Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

Рассмотрим, например, функцию, в которую вводят расстояние до массивного объекта, а в качестве результата получают величину гравитационного притяжения, порождаемого в данной точке этим массивным объектом. Ньютон осознал, что такое притяжение становится тем слабее, чем больше расстояние до объекта. Он открыл очень точное соотношение между величиной притяжения и расстоянием. Если я нахожусь на расстоянии х от планеты, то, согласно функции Ньютона, сила гравитационного притяжения пропорциональна 1/ х 2. Это так называемый закон обратных квадратов. Можно нарисовать график этой функции.

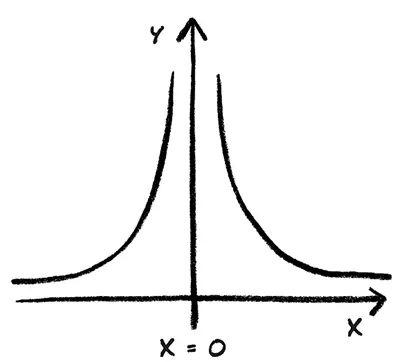
График функции 1/x 2 . Функция имеет сингулярность в точке x = 0

Однако при приближении к объекту происходит нечто интересное. Сила становится все больше и больше, пока мы не доходим до точки х = 0, в которой результат становится бесконечным, а на графике нельзя отложить значение. Разумеется, в реальности такое расстояние измеряется от центра планеты и при достижении ее поверхности функция и график изменяются, потому что после прохождения сквозь поверхность планеты разные ее части начинают оказывать притяжение в других направлениях. В центре тяжести планеты все разнонаправленные притяжения уравновешиваются и суммарное гравитационное притяжение равно нулю. Но что будет, если заменить планету на черную дыру, пространственную область, вся масса которой должна быть сосредоточена в единственной точке? Эта точка имеет бесконечную плотность, и при приближении к ней гравитационное притяжение становится бесконечным.

Тот факт, что данная функция не имеет смысла при х = 0, математики называют сингулярностью. Сингулярности бывают разные, но все они содержат точку, в которой функция не дает разумных результатов или имеет разрывный скачок от одного значения к другому.

Очень примитивный пример сингулярности можно получить, если взять монету и закрутить ее на столе. В отсутствие трения и сопротивления воздуха монета вечно продолжала бы вертеться с постоянной скоростью. Однако вследствие наличия рассеяния энергии монета вечно вертеться не будет. Вместо этого угол ее наклона к поверхности стола уменьшается, но, что интересно, пропорционально ему увеличивается скорость ее вращения. По мере приближения угла к нулю скорость в конце концов становится бесконечной. На последних стадиях вращения монета падает на стол, вибрируя и издавая жужжащий звук, частота которого быстро увеличивается, пока наконец дрожащая монета не останавливается.

Уравнения движения показывают, что скорость вращения монеты возрастает так, что через конечное количество времени она достигает бесконечного значения. Именно этот эффект мы слышим, когда увеличивается частота звука. Вертящаяся монета дает нам пример сингулярности. Разумеется, при этом действуют и другие эффекты, которые не допускают полного осуществления такой математической бесконечности, но этот пример показывает, что для получения бесконечности из физического уравнения не обязательно бросаться в черную дыру.

Даже Ньютоновы уравнения планетарного движения могут порождать сингулярности. Как я объяснял в конце первого «рубежа», математик Ся Чжихун показал, что четыре планеты можно расположить таким образом, что пятая планета будет вытолкнута из их среды и наберет бесконечную скорость за конечное время. Уравнения ничего не говорят о дальнейшей судьбе такой планеты, ожидающей ее после этой астрономической сингулярности.

Сингулярности обычно соответствуют моментам, в которые в игру вступает бесконечность и развитие событий после которых предсказать невозможно. Такие сингулярности могут возникать не только в физике. Известен пример статьи, которую опубликовали в 1960 г. Хайнц фон Фёрстер, Патриция Мора и Лоуренс Амиот, предсказывая серьезную сингулярность, которая должна произойти здесь, на Земле [96]. Если скорость роста населения и дальше будет следовать закономерностям, наблюдавшимся до 1960 г., то население нашей планеты должно стать бесконечным 13 ноября 2026 г. Особо отметим для суеверных, что этот день выпадет на пятницу.

Простейшая модель роста популяции утверждает, что этот рост имеет экспоненциальный характер. Например, численность некоторого вида может удваиваться каждые 50 лет. В такой модели популяция быстро разрастается, но никогда не становится бесконечной. Но анализ исторических данных, проведенный авторами этой статьи, говорил о том, что период удвоения численности человечества становится все короче и короче.