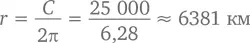Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Число π определяется как постоянная величина, представляющая собой соотношение длины круга к его диаметру. То есть

И π остается неизменным для абсолютно любой окружности! Если хотите, можете преобразовать эту формулу для подсчета длины окружности: зная диаметр D или радиус r той или иной окружности, вы можете просто посчитать

или

Цифровое выражение π начинается с

Чуть позже мы узнаем, что идет дальше, после 9, а заодно обсудим некоторые свойства этого числа.

Определить длину окружности «на глазок» не так-то легко. Испытайте себя – возьмите высокий стакан и постарайтесь прикинуть, что больше: его высота или длина окружности? Уверен, большинство проголосует за высоту… и почти наверняка вы окажетесь неправы: чаще всего больше будет именно длина окружности. Не верите? Проверить достаточно легко: просто измерьте большим и указательным пальцами диаметр стакана и трижды отложите этот отрезок вдоль его стенки.

Теперь можно смело отвечать на первый из двух вопросов, заданных в начале главы. Если мы представим экватор в виде идеального круга с длиной окружности, равной 40 075 км, его радиус составит

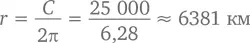
Но значение радиуса не так уж для нас и важно – куда важнее знать, насколько увеличится этот радиус, если к длине окружности прибавится три метра – совсем ненамного, примерно на 3/2π ≈ 0,5 метра. Следовательно, под веревкой окажется достаточно места, чтобы проползти, но недостаточно, чтобы пройти в полный рост (если, конечно, вы не танцор лимбо [21]).

Но самым удивительным здесь будет не столько сам ответ, сколько тот факт, что полученные нами 0,5 м ни капельки не зависят от изначальной длины окружности – вы придете к тому же результату независимо от того, обвязываете ли вы веревкой Землю, Юпитер, Плутон или теннисный мячик. Например, радиус круга с длиной окружности, равной 15 м, составит 15/(2π) ≈ 2,38. Прибавив 3 метра, получим новый радиус 18/(2π) ≈ ≈ 2,86, который будет больше старого примерно на 0,5 метра.

А вот еще один очень важный факт из геометрии окружностей.

Теорема:Предположим, что точки X и Y лежат на окружности строго друг напротив друга. Тогда при любом положении третьей точки P ∠ XPY = 90°.

На рисунке, например, хорошо видно, что углы ∠ XAY , ∠ XBY и ∠ XCY являются прямыми.

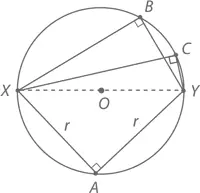
Доказательство:Проведем линию радиуса из точки O к точке P . Положим ∠ XPO = x , а ∠ YPO = y . Наша цель – показать, что x + y = 90°.

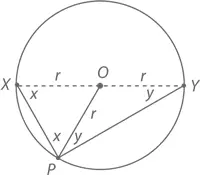
Так как отрезки OX и OP суть радиусы окружности, их длина равна r , следовательно, треугольник XPO будет равнобедренным. Согласно теореме о равнобедренных треугольниках, ∠ OXP = ∠ XPO = x . По той же логике отрезок OY является радиусом, а ∠ OYP = ∠ YPO = y . Поскольку сумма углов треугольника XYP должна быть равна 180°, получаем 2 x + 2 y = 180°, а значит, x + y = 90°, что и требовалось доказать.☺

Теорема эта является частным случаем другой, самой любимой моей во всей геометрии теоремы о центральном угле, которой посвящено следующее «Отступление».

Ответ на второй вопрос нашей мини-викторины может дать теорема о центральном угле . Возьмем две случайные точки X и Y , расположенные на окружности. Бóльшая дуга – это длинный путь от X и Y, меньшая – короткий путь. Теорема о центральном угле утверждает, что вне зависимости от положения точки P на большей дуге, проходящей от X к Y , размер угла ∠ XPY будет постоянным , а более конкретно – равным половине центрального угла ∠ XOY . Если при этом расположить на меньшей дуге точку Q , получим ∠ XQY = 180° – ∠ XPY .

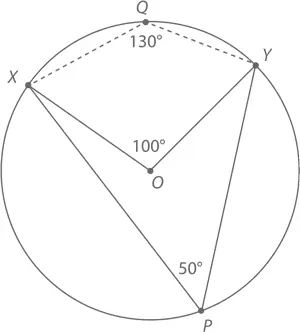
Например, если ∠ XOY = 100°, тогда при любом положении P на большей дуге, проходящей от X к Y , ∠ XPY = 50°, а при любом положении Q на меньшей дуге, проходящей от X к Y , ∠ XQY = 130°.