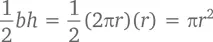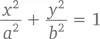Зная длину окружности, мы можем вывести очень важную формулу – формулу вычисления ее площади.
Теорема:Площадь круга с радиусом r равна π r ².
Вы наверняка помните эту формулу со школы. Что ж, тем больше удовольствия вы получите, узнав, наконец, из чего она вытекает. Конечно, правильнее всего было бы использовать метод вычислений, но пока вполне можно удовлетвориться и другим, не менее эффективным, доказательством.
Доказательство 1:Представьте себе круг как совокупность концентрически расходящихся колец, как это показано на рисунке. Сделайте в нем прорезь от верхнего края к центру, а затем «разогните» кольца, чтобы они сложились в фигуру, напоминающую треугольник. Чему будет равна площадь этой фигуры?
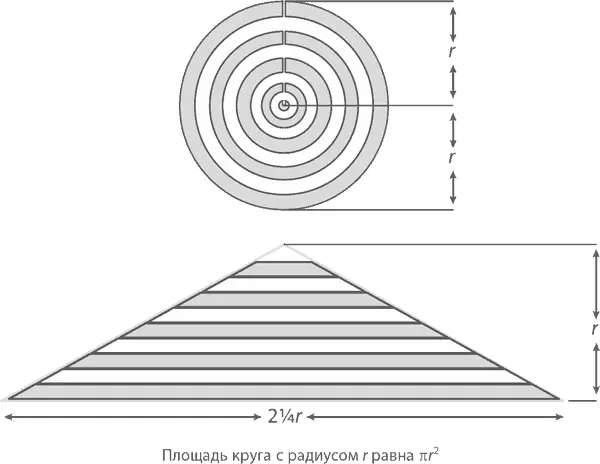
Надеюсь, вы не забыли, что площадь треугольника с основанием b и высотой h составляет 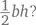 Основание получившейся у нас фигуры равно 2π r (длине окружности), а его высота – r (расстоянию от центра окружности до его нижнего края). Так как наш «очищенный» круг становится тем более треугольным, чем больше мы добавляем к нему колец, его площадь составляет
Основание получившейся у нас фигуры равно 2π r (длине окружности), а его высота – r (расстоянию от центра окружности до его нижнего края). Так как наш «очищенный» круг становится тем более треугольным, чем больше мы добавляем к нему колец, его площадь составляет
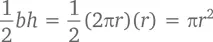
что и требовалось доказать.☺
Теорема эта настолько прекрасна, что просто невозможно устоять и не доказать ее еще раз. Только если в предыдущем случае мы чистили луковицу, теперь будем разрезать пиццу.
Доказательство 2:Разделите круг на четное количество равных секторов-«кусочков». Возьмите «кусочек» из верхней половинки и положите рядом с «кусочком» из нижней половинки, как показано на рисунках (в наших примерах мы разрезали «пиццу» сначала на 8, а потом – на 16 частей). Разложите так весь круг. С увеличением количества секторов форма каждого из них будет все больше и больше напоминать треугольник с высотой r . Чередование нижних секторов (назовем их «сталагмитами») с верхними («сталактитами») дает нам фигуру, по форме очень близкую к прямоугольнику, с шириной, равной r , и длиной, равной половине длины окружности, то есть π r . (Чтобы сделать ее именно прямоугольником, а не параллелограммом, «отсечем» от крайнего левого «сталактита» ровно половину и «приклеим» ее к правому краю.) Так как форма разделенного на сектора круга становится все более и более
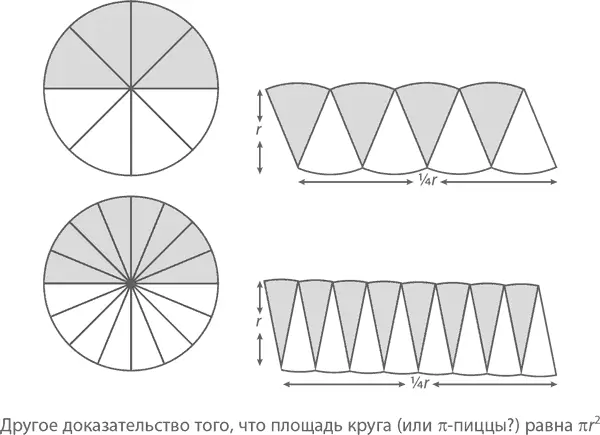
прямоугольной с увеличением количества этих секторов, площадь окружности составит
bh = (π r )( r ) = π r ²
как мы и предполагали.☺
А еще можно взять окружность и представить ее на плоскости в виде графика.
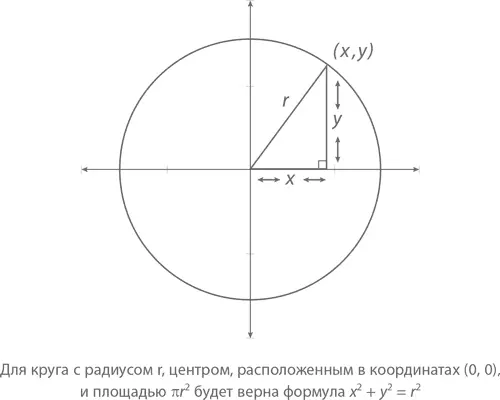
Для круга с радиусом r и центральной точкой, расположенной в координатах (0, 0) работает формула
x ² + y ² = r ²
что хорошо видно по графику чуть ниже. Чтобы в этом разобраться, возьмем некую лежащую на окружности точку с координатами ( x, y ). Опустим из нее до оси x перпендикулярную этой оси линию – получится прямоугольный треугольник с катетами x и y и гипотенузой r . Тогда, согласно теореме Пифагора, x ² + y ² = r ².
Круг с r = 1 называется единичным. Если мы «растянем» такой круг по горизонтали с коэффициентом a и по вертикали с коэффициентом b , получится эллипс (или овал) вроде этого:
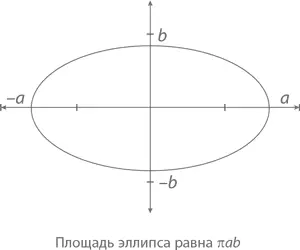
Подобная фигура имеет формулу
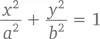
и площадь πab, что вполне логично, потому что площадь изначального единичного круга равняется π, после чего мы растянули ее на ab . Обратите внимание, что при a = b = r мы получим круг (а не эллипс) с радиусом r – π ab же, таким образом, превратится в π r ².
Существует несколько забавных фактов, связанных с эллипсами, которыми я хотел бы с вами поделиться. Например, вы можете нарисовать овал с помощью двух канцелярских кнопок, лески и карандаша.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


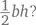 Основание получившейся у нас фигуры равно 2π r (длине окружности), а его высота – r (расстоянию от центра окружности до его нижнего края). Так как наш «очищенный» круг становится тем более треугольным, чем больше мы добавляем к нему колец, его площадь составляет
Основание получившейся у нас фигуры равно 2π r (длине окружности), а его высота – r (расстоянию от центра окружности до его нижнего края). Так как наш «очищенный» круг становится тем более треугольным, чем больше мы добавляем к нему колец, его площадь составляет