Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

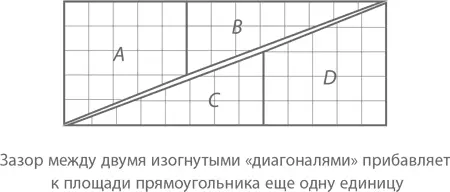
В этой главе мы узнали много интересного о треугольниках, квадратах, прямоугольниках и других полигонах, образованных с помощью разного количества прямых линий. Геометрия окружностей и других фигур изогнутой формы более сложна. Здесь нам не обойтись без тригонометрии и ее специфических методов счисления. И, конечно же, без основы основ – удивительного числа π.

Прошлую главу мы начали с проверки своей геометрической интуиции: речь шла сначала о прямоугольниках, затем – о треугольниках и наконец – о натянутой между двух футбольных ворот веревке. Пора поговорить и об окружностях, и тут уж мы мелочиться не будем – начнем с того, что обмотаем веревкой Землю!

Вопрос 1.Представьте себе веревку, достаточно длинную, чтобы обернуть ее вокруг Земли по экватору (это примерно 40 075 км). Но перед тем как завязать узелок, добавим к ней еще три метра. Так вот, если неким волшебным образом нам удастся поднять веревку над землей и водой по всей ее длине на одну и ту же высоту, какой будет эта высота?

А. Чуть больше пары сантиметров.

Б. Достаточной, чтобы под ней можно было проползти.

В. Достаточной, чтобы под ней можно было пройти в полный рост.

Г. Достаточной, чтобы под ней мог проехать грузовик.

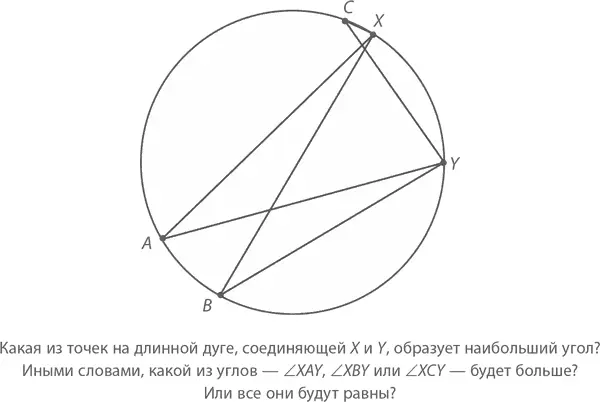
Вопрос 2.Две точки окружности – X и Y (см. рисунок) – соединяют две дуги: длинная и короткая. Допустим, что на большей (то есть длинной) дуге мы хотим поставить третью точку Z . Где именно она должна находиться, чтобы угол ∠ XZY был как можно больше?

А. В точке A (ровно напротив середины расстояния между XY ).

Б. В точке B (являющейся отражением точки X по линии, проходящей через центр круга).

В. В точке С (лежащей настолько близко к точке X , насколько возможно).

Г. Где угодно, потому что все углы будут абсолютно равны.

Чтобы ответить на эти вопросы, нужно разобраться в особенностях геометрии окружностей. Впрочем, если вам все это кажется смертельно скучным, можно вполне обойтись и так: ответом на первый вопрос будет вариант Б, на второй – вариант Г. Но разве вам интересно глотать пищу, не чувствуя ее вкуса? Так вот, особенности геометрии окружностей и есть тот самый вкус.

Любая окружность может быть выражена двумя понятиями – точкой O и положительной величиной r , причем точка O равноудалена от остальных точек окружности на расстояние, равное r (см. рисунок ниже). Точка O называется центром окружности. Расстояние r – радиусом окружности. А еще радиусом для удобства называется отрезок OP , проведенный от точки O к лежащей на линии круга точке P .

Диаметр окружности – это величина D, обозначающая расстояние между двумя максимально удаленными друг от друга точками окружности и определяющаяся как его удвоенный радиус. То есть

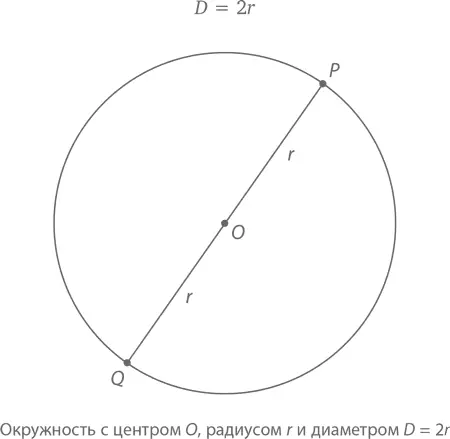
Периметр окружности (то есть расстояние, пройденное по кругу от некой точки до нее же) называется ее, окружности, длиной (или периферией) и обозначается буквой C . На рисунке хорошо видно, что C длиннее, чем 2 D , потому что идти по полукругу от точки P к точке Q придется явно дольше, чем напрямик по D , равно как и обратный путь от точки Q к точке P по другому полукругу займет больше времени. Следовательно, C > 2 D . А раз уж мы заметили это, почему бы нам не заметить, что C даже немного длиннее, чем 3 D . Правда, для того, чтобы наша уверенность была стопроцентной, придется надеть 3 D -очки… (извините, не сдержался ☺).

На самом деле для того, чтобы сопоставить длину окружности с ее диаметром, нам нужно «распрямить» круг, измерить получившуюся линию, а потом разделить результат на диаметр. И вы с удивлением обнаружите, что, независимо от того, измеряете вы монетку, дно стакана, тарелку или гимнастический круг, у вас всегда получится