Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

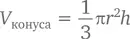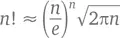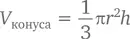
И хотя вычисления здесь и в самом деле совершенно не нужны, отказать себе в удовольствии, которое дарит нам эта красота и простота, совершенно невозможно: площадь поверхности конуса равна

Ну, и наконец, пицца, имеющая радиус z и толщину a , как видно на рисунке. Каков будет ее объем?

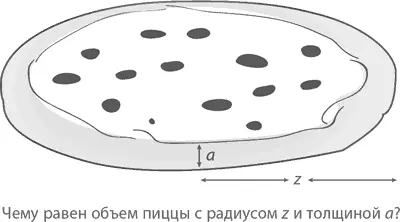
Это лакомство – не что иное, как необычной формы цилиндр (радиус z , высота a ), объем которого равен

Немного переделаем эту формулу – уверен, у вас слюнки потекут:

В том, что число π появляется в площадях и длинах всех кругообразных объектов, рассмотренных нами, ничего удивительного нет. Но только этим сфера его влияния не ограничивается – оно обнаруживается даже там, где, казалось бы, ему делать совершенно нечего.

Возьмем для примера множество n ! подробно рассмотренное нами в главе 4. Казалось бы, причем тут окружности, эллипсы и прочие подобные фигуры и объекты – ведь оно нужно исключительно для того, чтобы подсчитывать дискретные величины. Мы знаем, что значение его вырастает стремительно, причем настолько, что до сих пор нет ни одного более или менее удобного и легкого способа его просчитать. Например, чтобы вычислить значение 100 000! нам потребуется несколько тысяч операций умножения. И все-таки один способ есть – столь же хитрый, сколь и полезный. Основан он на формуле Стирлинга, которая выглядит как

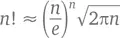
и в которой e = 2,71828… ( e – это еще одно важное иррациональное число, которое ждет вашего внимания в главе 10). Компьютер может подсчитать это до четырех значащих цифр – например, 64! = 1,269 × 10 89. А согласно формуле Стирлинга, 64! ≈ (64/ e ) 64√( 128π ) = 1,267 × 10 89. (Есть ли легкий способ возвести число в 64-ю степень? Да, есть! Поскольку 64 = 2 6, нам нужно взять 64/ e и возвести его в квадрат шесть раз.)

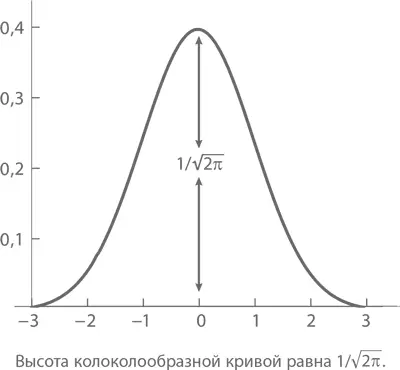
Знаменитая колоколообразная (или гауссова ) кривая , активно использующаяся в статистических исследованиях и некоторых экспериментальных науках, имеет высоту 1/√( 2π ) (подробнее о ней – в главе 10).

Встречается число π и в бесконечных суммах: как впервые наглядно показал Леонард Эйлер, сложение квадратов обратных величин положительных целых значений дает нам

А если мы повторно возведем в квадрат каждое из значений выше, сумма обратных величин четвертой степени окажется равной

Формулу эту можно обобщить, распространив на любой ряд обратных величин всех четных степеней основания числа 2 k . В ответе будет фигурировать π 2 k , умноженное на рациональное число.

А что насчет нечетных обратных величин? В главе 12 мы увидим, что сумма обратных величин положительных значений бесконечна. При любой нечетной степени больше 1 получим что-то наподобие этого:

(это пример для кубов). Сумма здесь будет, по идее, конечной, вот только простой формулы для ее точного вычисления пока никто не нашел.

Невероятно, но факт: π всплывает даже в задачах, связанных с вероятностью. Например, если вы выберете два случайных больших числа, вероятность того, что у них не будет ни одного общего простого множителя, составит чуть больше 60 %. Это приблизительно. А если точно, то 6/π² = 0,6079…. И то, что этот результат является обратной величиной для одной из посчитанных нами чуть выше бесконечных сумм – вовсе не совпадение.

К тому, что число π немного превышает 3, вы вполне можете прийти самостоятельно – для этого достаточно просто аккуратно все подсчитать. Но сначала нужно найти ответы на парочку вопросов. Во-первых, можно ли доказать соседство π и 3, не проводя специальных измерений? Во-вторых, существует ли для π какое-нибудь более удобоваримое представление (скажем, формула или простая дробь)?