Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Я уже не раз говорил, что многие числовые закономерности, в которых присутствуют числа Фибоначчи, суть настоящая поэзия. И это не просто метафора: эти числа действительно используются при создании стихотворений. Возьмем, к примеру, лимерики. Вот, последите за ритмом (пусть без слов, просто используя сетку слогов):

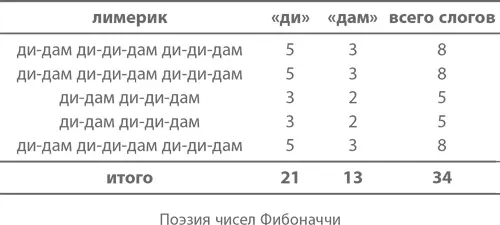
Если посчитать количество слогов в каждом ряду, мы получим числа Фибоначчи! Лично меня это вдохновило настолько, что я отважился написать о них свой собственный лимерик:

Одна из главных радостей занятий математикой – возможность окончательных, не оставляющих ни тени сомнения доказательств. Это ставит математику на особое место в ряду других наук, которые опираются на соответствие законам материального мира. Однако новые открытия могут опровергать или изменять эти законы. В математике же доказанное однажды остается доказанным навсегда. Прошло больше 2000 лет с того момента, как Евклид доказал бесконечность множества простых чисел – и это никогда не удастся оспорить. Научно-технические формации сменяют друг друга, теоремы же вечны. Как однажды сказал великий Годфри Харди [15]: «Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они сотканы из идей». По-моему, доказать новую теорему – все равно что шагнуть на тропу, ведущую в научное бессмертие.

В математике доказывают не только абсолютную истинность, но и невозможность . Часто приходится слышать: «Нельзя доказать невозможное». Полагаю, здесь имеется в виду, что никому не под силу доказать существование розовых коров – по крайней мере, до тех пор, пока мы не увидим их в один прекрасный день. Но в математике невозможное вполне себе доказуемо . Например, сколько ни пытайтесь, вы ни за что не найдете два четных числа, которые в сумме давали бы нечетное. Или простое число, которое было бы больше всех остальных простых чисел. Сложность таких доказательств поначалу пугает, к ним нужно привыкнуть, и не ждите, что это произойдет с первого (а то и со второго или с третьего) раза. Но стоит войти во вкус – и удержаться уже невозможно: настолько они удивительны и притягательны. Стройное доказательство подобно хорошему анекдоту или уместной шутке – удовлетворение от него испытываешь ничуть не меньшее.

С вашего позволения, расскажу о первом своем опыте на этой стезе. В детстве двумя главными предметами моего обожания были настольные игры и загадки. Как-то раз мой друг предложил мне загадку, связанную с настольными играми, и, конечно, я был заинтригован. Он положил передо мной пустую шахматную доску размером 8 на 8 клеточек и 32 костяшки домино и спросил:

– Можешь выложить домино так, чтобы они закрыли всю доску?

– Конечно, – уверенно ответил я. – Просто по четыре костяшки на ряд. Вот так:

– Молодец, – сказал он. – А если я уберу две клетки – правую нижнюю и левую верхнюю, и их останется 62 – сможешь закрыть оставшиеся 31 костяшкой? – и он положил на крайние квадратики две монетки.

– Хм… Наверное, – ответил я.

Но как я ни пытался, какие комбинации ни пробовал, у меня ничего не получалось. Наконец я сдался, заявив, что это в принципе невозможно.

– А если невозможно, – сказал мой друг, – можешь доказать это?

Я не мог. Ведь для этого потребовалось бы проверить бесконечное множество вариантов (если хотите, можете посчитать, сколько именно) и удостовериться в том, что каждый из них невозможен.

– Посмотри на цвета, – посоветовал друг, видя мое замешательство.

«На цвета? Причем тут цвета?» – подумал я. А потом понял. Обе закрытые клеточки были белыми, а значит, из 62 оставшихся свободными, 32 были черными и всего лишь 30 – белыми. А поскольку костяшка домино, как ее ни положи, закрывает пару разноцветных клеточек, выложить ими всю доску не получилось бы ни за что на свете. Здо́рово!