А теперь – мой самый любимый факт о числах Фибоначчи. Он касается наибольшего общего делителя (НОД). Наибольший общий делитель двух чисел есть наибольшее число, на которое делятся оба эти числа. Например, для 20 и 90 НОД равен 10. Обозначается это как
НОД(20, 90) = 10
Как вы думаете, каким будет наибольший общий делитель двадцатого и девяностого чисел последовательности Фибоначчи? Ответ звучит как поэзия: 55 – десятое число последовательности Фибоначчи! А вот уравнение:
НОД( F 20, F 90) = F 10
Или в общем виде, для значений m и n :
НОД( F m, F n ) = F НОД( m; n )
Другими словами, «НОД значений F есть значение F НОДа»! Подробно останавливаться на этом мы здесь не будем, но и пройти мимо я не мог.
Иногда закономерность может оказаться обманчивой. Какие, например, из чисел Фибоначчи являются простыми? (Простые – это числа больше 1, которые при этом делятся без остатка только на 1 и на самих себя, мы поговорим о них подробнее в следующей главе.) Числа больше единицы, не являющиеся простыми, называются составными , потому что их можно разложить на неделимые простые составляющие. Вот несколько первых простых чисел последовательности Фибоначчи:
2, 3, 5, 7, 11, 13, 17, 19…
А теперь взгляните на числа, стоящие на «простых» позициях:
F 2= 1, F 3= 2, F 5= 5, F 7= 13, F 11= 89, F 13= 233, F 17= 1597
Числа 2, 5, 13, 89, 233 и 1597 – простые. Закономерность вроде бы говорит нам о том, что, если значение p > 2 является простым, простым будет и F p. Однако следующий же элемент последовательности эту закономерность нарушает: F 19= 4181 – уже составное число, потому что 4181 = 37 × 113. Но верно и то, что каждое простое число больше 3 стоит в последовательности Фибоначчи на «простой» позиции. Это следует из одной из уже рассмотренных закономерностей. F 14должно быть составным, поскольку каждое седьмое число последовательности кратно F 7= 13 (и правда: F 14= 377 = 13 × 29).
На самом деле простые числа Фибоначчи встречаются редко – пока что официально подтверждено лишь 33, наибольшее из них занимает F 81839позицию. И это притом, что вопрос, является ли количество простых чисел в последовательности бесконечным, еще не решен.
Но отвлечемся немного от серьезных научных изысканий и займемся небольшим, но забавным фокусом, основанным на магии чисел Фибоначчи.

В 1 и 2 рядах таблицы напишите два любых числа от 1 до 10. Сложите их, а сумму запишите в 3 ряду. Затем сложите числа из 2 и 3 рядов. Результат запишите в 4 ряд. Продолжайте так делать (ряд 3 + ряд 4 = ряд 5 и т. п.), пока не дойдете до конца таблицы. У вас получится свой вариант последовательности Фибоначчи. А теперь разделите число из 10 ряда на число из 9 ряда. Из результата вам нужны первые три цифры, включая те, которые идут после запятой. В нашем примере 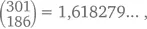 из них оставляем 1,61. Хотите – верьте, хотите – нет, но, с каких бы двух положительных (необязательно целых и даже необязательно из промежутка от 1 до 10) чисел в 1 и 2 рядах вы ни начали, частным при делении числа 10 ряда на число 9 ряда всегда будет 1,61. Попробуйте сами разок-другой и легко в этом убедитесь.
из них оставляем 1,61. Хотите – верьте, хотите – нет, но, с каких бы двух положительных (необязательно целых и даже необязательно из промежутка от 1 до 10) чисел в 1 и 2 рядах вы ни начали, частным при делении числа 10 ряда на число 9 ряда всегда будет 1,61. Попробуйте сами разок-другой и легко в этом убедитесь.
Чтобы разобраться в природе этого фокуса, обозначим первые два числа литерами x и y . Тогда, следуя методу Фибоначчи, получаем x + y в 3 ряду, y + ( x + y ) = x + 2 y в 4-м и т. д. по таблице:

Требуется найти частное чисел 10 и 9 рядов:
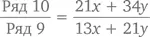
Почему же результат всегда будет начинаться с 1,61? Вы удивитесь, но в основе этого лежит неправильное сложение дробей. Допустим, у нас есть две дроби: a/b и c/d , причем знаменатели b и d – положительные величины. Что будет, если сложить между собой сначала числители, а потом знаменатели? А будет то, что получившееся в результате число, называемое медиантой , всегда будет где-то между двух исходных дробей. То есть при любых дробях a / b < c / d, знаменатели которых суть положительные величины, имеем
Читать дальше
Конец ознакомительного отрывка
Купить книгу


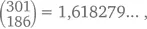 из них оставляем 1,61. Хотите – верьте, хотите – нет, но, с каких бы двух положительных (необязательно целых и даже необязательно из промежутка от 1 до 10) чисел в 1 и 2 рядах вы ни начали, частным при делении числа 10 ряда на число 9 ряда всегда будет 1,61. Попробуйте сами разок-другой и легко в этом убедитесь.
из них оставляем 1,61. Хотите – верьте, хотите – нет, но, с каких бы двух положительных (необязательно целых и даже необязательно из промежутка от 1 до 10) чисел в 1 и 2 рядах вы ни начали, частным при делении числа 10 ряда на число 9 ряда всегда будет 1,61. Попробуйте сами разок-другой и легко в этом убедитесь.