Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Теорема:Среднее арифметическое двух рациональных чисел также будет рациональным числом.

Доказательство:Возьмем два рациональных числа – x и y . Значит, в равенствах x = a / b и y = c / d значения a, b, c и d суть целые числа. Среднее арифметическое x и y, таким образом, можно представить как

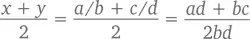
Это дробь, числитель и знаменатель которой – целые числа. Следовательно, среднее арифметическое значение x и y является рациональным числом.

А теперь давайте подумаем, что же именно утверждается в этой теореме. А утверждается в ней то, что между двумя разными рациональными числами, насколько бы близки они друг другу ни были, всегда найдется еще одно рациональное число. Возникает искушение сделать из этого вывод, что все числа являются рациональными (как довольно долго думали древние греки). Нет, это не так. И смотрите, почему. Возьмем число √ 2, которое в десятичной записи выглядит как 1,4142… Если мы попробуем записать его как обычную дробь, получится что-нибудь вроде 10/7 или 1414/1000 (вариантов огромное множество), но все они будут приблизительными и никогда при возведении в квадрат не дадут 2. Но что, если мы просто плохо ищем? Да нет, не плохо, и следующая наша теорема как раз и показывает, что любые такие поиски бесполезны по определению. Доказательство будет строиться от противного, как это обычно и бывает, когда разговор заходит об иррациональных числах. А заодно мы увидим, как сократить дробь до ее несократимого значения – того предела, когда у числителя и знаменателя остается только один общий делитель – 1.

Теорема:√ 2 есть иррациональное число.

Доказательство:Предположим обратное: √ 2 есть число рациональное. В таком случае существуют некие положительные целые числа a и b , для которых верно, что

где дробь a / b – несократимая. Возведя обе части уравнения в квадрат, получим

или

что приводит нас к тому, что a ² есть четное целое число. А если a ² – четное, значит, четным является и a (по аналогии с недавним нашим доказательством того, что, если нечетное a умножить на само себя, результат будет также нечетным). То есть a = 2 k , где k – целое число. Добавим это в свое уравнение и получим

То есть

что приводит нас к

и констатации того факта, что b ² является четным числом. Значит, четным должно быть и b . Но постойте! Ведь при четных значениях как a , так и b дробь a / b никак не может быть несократимой! Это противоречит нашим исходным условиям. И завело нас в эту ловушку предположение, что √ 2 является рациональным числом. Поэтому нам не остается ничего иного, кроме как признать: число √ 2 – иррациональное.☺

Лично я нахожу это доказательство восхитительным (и смайлик в конце строки тому подтверждение): прямая и хорошо освещенная тропа чистой, ничем не замутненной логики приводит нас к удивительному умозаключению. В главе 12 мы еще увидим, насколько велик на самом деле процент иррациональных чисел. Практически все действительные числа являются иррациональными, притом, что в повседневной жизни мы с ними почти не сталкиваемся.

Из доказанной нами только что теоремы следует одно любопытное заключение (его, пожалуй, даже можно назвать сопутствующей теоремой – такой, условия которой вытекают из только что доказанной). Основано оно на следующем правиле возведения в степень, согласно которому для любых положительных значений a, b и c

То есть утверждение, что (5³)² = 5 6, будет вполне справедливым, потому что

Сопутствующая теорема:Существуют иррациональные числа a и b , при которых число a b будет рациональным.

Не пугайтесь, нам эта теорема вполне по плечу, хоть мы и знаем пока лишь одно иррациональное число – √ 2 . Приведенное ниже доказательство является, по сути, доказательством существования: мы же пытаемся просто узнать, есть ли вообще такие a и b , а не определить их конкретные числовые выражения.