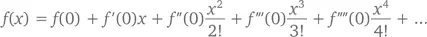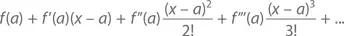Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Последовательно дифференцируя x – x 3/3! + x 5/5! – x 7/7! +…, получаем 1 – x 2/2! + x 4/4! – x 6/6! +…, что соотносится с тем, что производная синуса – это косинус. Справедливо и обратное: производная косинуса – это синус со знаком минус. А еще этот ряд лишний раз доказывает, что cos 0 = 1, и поскольку каждая степень в нем выражена четным числом, значение cos (– x ) будет равно cos x . Впрочем, нам это уже известно (например, (– x ) 4/4! = x 4/4!). Следуя той же логике, мы можем прийти к sin 0 = 0, а поскольку каждая степень выражена нечетным числом, sin (– x ) = –sin x , как мы и предполагали.

Теперь давайте попытаемся понять, откуда, собственно говоря, берутся эти формулы. Мы знаем, как найти производные наиболее популярных функций. Но бывают такие ситуации, когда одну и ту же функцию нужно продифференцировать несколько раз, разыскав ее вторую ( f'' ( x )), третью ( f''' ( x )) и т. д. производную. f'' ( x ) выражает крутизну наклона функции (то есть ее вогнутость ) в точке ( x, f ( x )), f''' ( x ) делает то же для второй производной и т. д.

Для этого имеются специальные формулы. Они называются рядами Тейлора , потому что первым, кто ввел их в оборот, был английский математик Брук Тейлор (1685–1731). Для функции f ( x ) с производными f' ( x ), f'' ( x ), f''' ( x ) и т. д. мы имеем

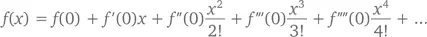
при любом значении x , «достаточно близком» к 0. Что значит «достаточно близком»? В некоторых функциях – например, ex , sin x или cos x – x может быть практически любой величиной. Но есть и такие функции (мы встретимся с ними чуть позже), которые имеют смысл только при очень маленьких значениях x .

Проследим, как меняется формула для f ( x ) = e x . Так как e x равна своей собственной первой (равно как и второй, и третьей и т. д.) производной, следовательно

то есть ряд Тейлора для ex превращается в 1 + x + x 2/2! + x 3/3! + x 4/4! +…, как и предполагалось. При небольшом значении x нам достаточно посчитать лишь несколько членов ряда, чтобы получить точную аппроксимацию верного ответа.

Посчитаем с его помощью проценты. Как мы выяснили в прошлой главе, если положить на счет $1000 под 5 %, то, при условии непрерывных начислений, к концу года мы будем иметь $1000 e 0,05= $1051,27. И мы знаем, как это подсчитать. Но к тому же ответу можно прийти и с помощью формул сначала второго –

а потом и третьего порядка аппроксимации : $1051,27.

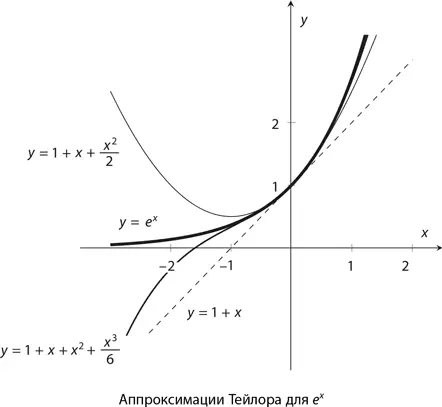
Аппроксимации Тейлора могут быть представлены в виде графика, на котором вместе с первыми тремя многочленами Тейлора изображена показательная (экспоненциальная) функция y = e x .

Постепенно увеличивая степень многочлена, мы достигаем все большей точности аппроксимации, особенно если x близок к 0. Но что же такого особенного в многочленах Тейлора, что делает их настолько эффективными? Аппроксимация первого порядка (называемая линейной ) утверждает, что при x , близком к 0,

На графике получается прямая линия, проходящая через точку (0, f (0)) с наклоном f' (0). Значит, многочлен Тейлора степени n будет проходить через ту же точку (0, f (0)) и иметь такие же первую, вторую, третью и т. д., вплоть до n -ной, производные, что и начальная функция f ( x ).

Кстати, многочлены и ряды Тейлора отлично показывают себя при работе и с другими величинами (не только 0), к которым стремится х . Так, ряд Тейлора для f ( x ) с начальной точкой a равен

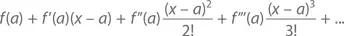
При a = 0 он будет равен f ( x ) для всех действительных или комплексных значений x , близких к a .

Возьмем ряд Тейлора для f ( x ) = sin x . Посмотрите: f' ( x ) = cos x, f'' ( x ) = –sin x, f''' ( x ) = –cos x , а f'''' ( x ) = sin x = f ( x ). При сопоставлении с 0, начав с f (0), мы придем к циклу 0, 1, 0, –1, 0, 1, 0, –1…., в котором каждое четное значение x попросту исчезает из ряда. Следовательно, получается, что при любом x , выраженном в радианах,