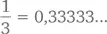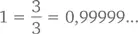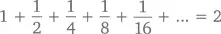Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Кстати, количества, выражаемые как ∞ – ∞ (бесконечность минус бесконечность) или 1/0 являются неопределенными. Конечно, очень велико искушение заявить, что 1/0 = ∞, потому что при делении единицы на все меньшую и меньшую положительную величину частное будет расти. Но ведь если делить 1 на все меньшие и меньшие по абсолютной величине отрицательные числа, то частное будет представать все большим и большим по абсолютной величине отрицательным числом.

Начнем, пожалуй, с утверждения, принимаемого всеми математиками и кажущегося неправильным большинству непосвященных:

То, что две эти величины очень близки друг к другу, не вызывает сомнений практически ни у кого. Но считать их одним и тем же числом?.. Несколько чересчур, правда? Неправда. Позвольте мне попробовать убедить вас в обратном. Поверьте, доказательств у меня так много, что хотя бы одно из них обязательно покажется вам правдоподобным.

Самое, пожалуй, простое исходит из утверждения, что

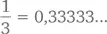
Умножаем обе стороны на 3 и получаем

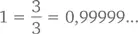
Другое доказательство основано на методе, который мы использовали в главе 6 для периодических десятичных дробей. Обозначим бесконечную последовательность знаков после запятой переменной w , вот так:

Умножим обе части на 10:

Вычтем первое уравнение из второго

и получим w = 1.

А вот доказательство, для которого алгебра вообще не нужна. Надеюсь, вы согласны с тем, что два числа могут считаться разными, если между ними расположено третье число, не равное ни первому, ни второму (например, их среднее арифметическое)? Пойдем от обратного: предположим, что 0,99999… и 1 суть разные величины. Какое же тогда число будет между ними? А если такого числа нет, значит, мы не можем утверждать, что они разные.

Два числа или две бесконечные суммы считаются равными в том случае, если они сколь угодно близки друг к другу, то есть разница между ними меньше любой положительной величины, будь то 0,1 или 0,0000001, или 1, деленное на триллион. Разница между 1 и 0,99999… – наглядный тому пример, и именно это дает математикам право утверждать, что 1 и 0,99999… суть одно и то же число.

Следуя той же логике, мы можем оценить бесконечную сумму следующего ряда:

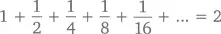
А еще мы можем найти ей физическое соответствие. Представьте, что вы стоите в двух метрах от кирпичной стены. Вы делаете шаг вперед – ровно на метр. Следующий шаг будет вполовину короче – полметра. Потом четверть метра, одна восьмая метра и так далее. С каждым шагом расстояние между вами и стеной сокращается ровно вполовину. Если проигнорировать физические ограничения на длину каждого следующего шага (в том числе и длину ваших ступней), то рано или поздно вы подберетесь вплотную к стене. Всего же вы пройдете ровно 2 метра.

То же можно представить и геометрически. Начнем с прямоугольника с длинами сторон 1 и 2 и площадью 2. Разделим его пополам, потом еще раз и еще – и так до бесконечности. Площадь первого сектора будет равна 1, второго – 1/2, третьего – 1/4 и так далее. Даже когда мы будем делить на n , стремящееся к бесконечности, мы не выйдем за пределы начального прямоугольника, а площади всех его секторов в сумме будут по-прежнему равны 2.

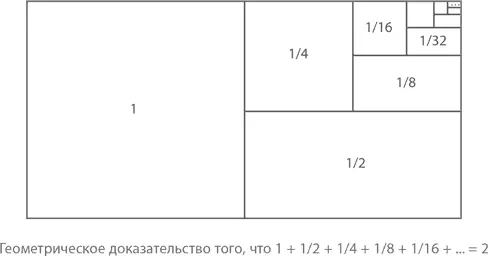
Алгебра позволяет нам подойти к решению задачи с точки зрения частичных , промежуточных сумм:

Эта закономерность подсказывает нам, что при n ≥ 0

Доказать это можно либо с помощью метода индукции (см. главу 6), либо как частный случай формулы конечного геометрического ряда.

Теорема (конечный геометрический ряд):При x ≠ 1 и n ≥ 0