Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

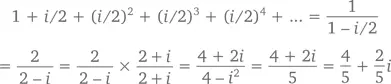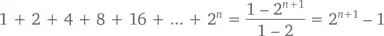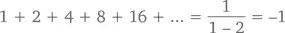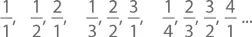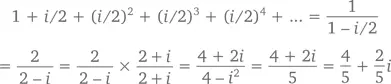
что показано на следующем графике, расположенном на комплексной плоскости.

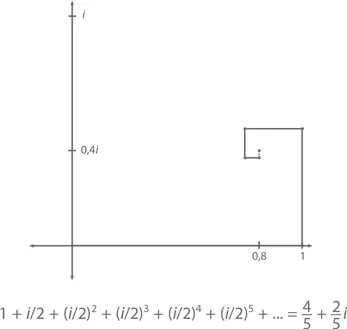
И хотя формула конечного геометрического ряда верна для любого значения x ≠ 1, (бесконечный) геометрический ряд требует, чтобы | x | был меньше 1. Например, при x = 2 конечный геометрический ряд покажет нам (как мы уже выяснили в шестой главе), что

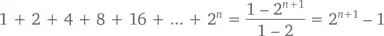
а бесконечный – что

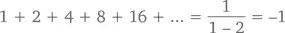
что выглядит нелепо (хотя это впечатление может быть и обманчивым: в предпоследнем разделе этой главы мы увидим вполне правдоподобное объяснение такого результата).

Число положительных целых величин бесконечно:

Равно как бесконечно и количество положительных четных целых величин:

Считается, что первое множество (или число элементов, или степень бесконечности) приблизительно равно первому. В пользу этого утверждения говорит тот факт, что положительные целые и положительные четные целые можно объединить в пары, вот так:

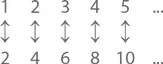
Множество, способное к объединению в пары, называется счетным . Степень бесконечности у него, как правило, невелика. Любое множество, величины которого можно перечислить , является счетным, так как первый его элемент есть пара к 1, второй – к 2 и т. д. Множество всех целых величин

перечислить от меньшего значения к большему не получится просто потому, что нет никакого «стартового» наименьшего значения. Зато получится перечислить их вот так:

Следовательно, множество всех целых является счетным, а число его элементов равно числу элементов в множестве положительных целых.

А что насчет множества положительных рациональных величин? Напомню: рациональными называются числа, имеющие форму m / n , где и m , и n суть положительные целые. Хотите – верьте, хотите – нет, но и это множество будет счетным. Перечислить его элементы можно следующим образом:

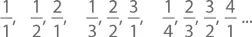
то есть мы берем дроби в соответствии с суммой их числителей и знаменателей. Так как любая рациональная величина неизбежно появляется в списке, их множество будет счетным.

А существуют ли вообще такие бесконечные множества, которые не являются счетными? Немецкий математик Георг Кантор (1845–1918) доказал, что все действительные величины, даже только те из них, что ограничены диапазоном от 0 до 1, образуют несчетное множество. Можно, конечно, попробовать перечислить их следующим образом:

и т. д. Но так мы никогда не выйдем за пределы величин с конечным количеством знаков. Число 1/3 = 0,333…, например, в нашем списке так и не встретится. Но, может, есть какой-нибудь другой, более эффективный способ перечисления? Кантор доказал, что его нет. Он пошел от обратного – предположил, что множество действительных величин является счетным. Он взял конкретный пример и начал с

Доказать, что этот список не будет полным, можно, «придумав» такое действительное число, которое никогда в нем не появится. Можно взять, скажем, величину 0, r 1 r 2 r 3 r 4…, где r 1есть целое в интервале от 0 до 9, которое отличается от первого числа только первой цифрой (в нашем примере r 1≠ 3). Так же обстоит и с r 2: оно отличается от второго числа второй цифрой (у нас r 2≠ 7). И так далее. Таким образом у нас может получиться, скажем, 0,2674… – число, которое никогда не появится в списке, даже на миллионной позиции, потому что будет отличаться от нее миллионной цифрой. А значит, какой бы список вы ни создавали, всегда будут такие величины, которые в нем не появятся, следовательно, множество действительных чисел является несчетным.