Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Рис. 111

Первым открытием Мандельброта была важность самоподобия – того факта, что многие природные формы представляют собой бесконечную последовательность мотивов, повторяющих сами себя внутри других таких же мотивов на разных масштабах. Великолепный пример проявления этого качества – раковина наутилуса (рис. 4), как, впрочем, и самая обычная цветная капуста: если отламывать от кочана соцветия, а от них – кусочки все меньше и меньше, они до какого-то предела все равно будут точным подобием целого кочана. Сфотографируйте камешек, отколовшийся от скалы, и вам, возможно, не удастся отличить снимок от фотографии целого утеса. Этим свойством обладает и непрерывная дробь, если ее напечатать (рис. 112): увеличьте еле видные циферки, и вы обнаружите всю ту же непрерывную дробь. Однако во всех этих случаях увеличение масштаба не сглаживает некоторых шероховатостей. Более того, неправильность характерна для любого масштаба.

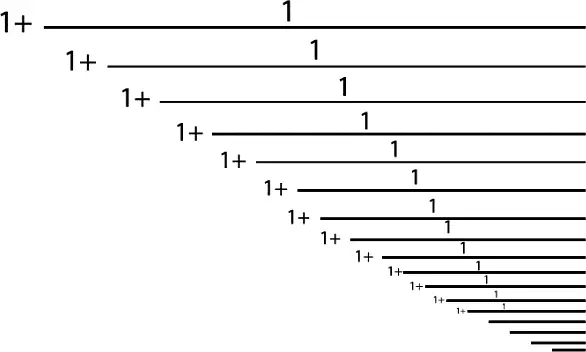
Рис. 112

Тогда Мандельброт задался вопросом: как определить измерения предмета, обладающего подобной фрактальной структурой? В мире евклидовой геометрии у любого предмета есть измерения, которые можно выразить целыми числами. У точки число измерений – нуль, у прямой – одно, у плоских фигур вроде треугольников и пятиугольников – два, у объемных тел вроде сфер и платоновых многогранников – три. А фрактальные кривые вроде молнии, с другой стороны, так агрессивно изгибаются туда-сюда, что попадают куда-то между одним и двумя измерениями. Если след молнии относительно гладкий, можно представить себе, что число фрактальных измерений близко к единице, если же он очень извилистый, следует ожидать числа измерений, близкого к двум. Все эти размышления вылились в вопрос, сделавшийся в наши дни знаменитым: «Какова длина побережья Британии?» Мандельброт дал на это неожиданный ответ: длина береговой линии, оказывается, зависит от длины линейки, которую возьмет измеряющий. Представьте себе, что вы начинаете со спутниковой карты Британии со стороной в один фут. Измеряете длину побережья, умножаете на нужный коэффициент, исходя из заданного масштаба карты. При таком методе, разумеется, пропадут всякие мелкие извивы береговой линии, которых на карте не видно. Теперь представьте себе, что вы вооружаетесь палкой метровой длины и начинаете долгое путешествие вдоль берегов Британии, тщательно измеряя береговую линию метр за метром. Результат, несомненно, будет гораздо больше прежнего, поскольку вам удастся зафиксировать куда более мелкие извивы и повороты. Однако вы наверняка заметите, что на более мелких участках вы все равно упустите какие-то подробности. Дело в том, что чем меньше будет наша линейка, тем больше окажется результат измерений, потому что всегда оказывается, что при уменьшении масштаба выявляется подструктура. Из этого следует, что, если имеешь дело с фракталами, нуждается в пересмотре даже концепция длины как средства передачи расстояния. Контуры береговой линии при увеличении не становятся прямыми, изгибы присутствуют при любом масштабе, и общая ее длина возрастает бесконечно – по крайней мере, пока мы не дойдем до атомов.

Рис. 113

Прекрасный пример такой ситуации – линия, которую можно считать очертаниями берегов некоей воображаемой страны. Снежинка Коха – кривая, которую первым описал в 1904 году шведский математик Нильс Хельге фон Кох (1870–1924) (рис. 113). Начертим равносторонний треугольник со стороной в один дюйм. Теперь в середине каждой стороны достроим треугольники поменьше – со стороной в одну треть дюйма. В результате на этом этапе у нас получится звезда Давида. Обратите внимание, что периметр первоначального треугольника составлял три дюйма, а теперь он состоит из двенадцати сегментов по трети дюйма каждый, так что общая его длина равняется уже четырем дюймам. Теперь будем последовательно повторять эту процедуру – на каждой стороне треугольника будем достраивать новый с длиной стороны в одну треть предыдущей. Каждый раз длина периметра будет возрастать с коэффициентом 4/3, и так до бесконечности, несмотря на то что линия ограничивает замкнутое пространство конечной площади (можно доказать, что площадь стремится к 8/5 площади первоначального треугольника).