Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Рис. 96

Теснее всего из всех геометрических фигур с золотым сечением связан, конечно, правильный пятиугольник, обладающий пятисторонней симметрией. Однако одними правильными пятиугольниками плоскость не замостишь, периодического узора не получится. Сколько ни старайся, останутся незаполненные промежутки. Поэтому долгое время считалось, что невозможно создать замощение с крупномасштабной упорядоченностью (так называемым «дальним порядком»), обладающее пятисторонней симметрией. Однако Роджер Пенроуз в 1974 году обнаружил два основных набора плиток, при помощи сочетания которых можно замостить плоскость целиком, соблюдая при этом «запретную» пятистороннюю симметрию. Получившиеся узоры не строго периодичны, хотя и обладают дальним порядком.

Мозаики Пенроуза, можно сказать, сплошь построены на золотом сечении. Одна из пар плиток, которые рассматривал Пенроуз, состоит из двух фигур под названием «дротик» и «змей» (рис. 97, a и b соответственно). Обратите внимание, что обе фигуры состоят из двух равнобедренных треугольников, входящих в состав правильного пятиугольника (рис. 25). Треугольник, у которого отношение стороны к основанию равно φ, – это так называемый золотой треугольник (рис. 97, b ), а треугольник, у которого отношение стороны к основанию равно 1/φ, – это золотой гномон (рис. 97, a ). Эти фигуры можно получить, если разделить в золотом сечении длинную диагональ ромба с углами 72 и 108 градусов (рис. 98).

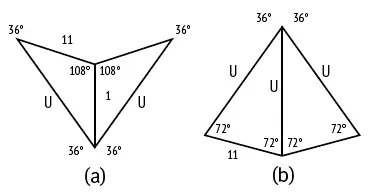
Рис. 97

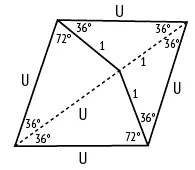
Рис. 98

Пенроуз и принстонский математик Джон Хортон Конвей показали, что для того, чтобы замостить плоскость змеями и дротиками непериодическим образом, как на рис. 99, нужно соблюдать определенные правила сочетаемости. Для этого удобно наносить на стороны фигур «метки» в виде выступов и пазов, как на кусочки паззла (рис. 100). Далее Пенроуз и Конвей доказали, что змеи и дротики могут непериодически заполнять плоскость бесконечным множеством способов, поскольку каждый узор можно окружить любым другим узором и таким образом создать третий, отличающийся от первых двух. Одно из самых поразительных свойств любой мозаики Пенроуза из дротиков и змеев состоит в том, что количество змеев примерно в 1,618 раз больше количества дротиков. То есть, если мы обозначим количество змеев как N змеев , а количество дротиков как N дротиков , то чем больше площадь, тем ближе отношение N змеев / N дротиков к числу φ.

Рис. 99

Рис. 100

Другая пара Пенроуза, непериодически заполняющая плоскость целиком, состоит из двух ромбов, «толстого» и «тонкого» (рис. 101). Как и пара «змей-дротик», каждый из ромбов состоит из двух золотых треугольников или двух золотых гномонов (рис. 102), и при замощении плоскости нужно соблюдать определенные правила сочетаемости, для удобства чего на нашем рисунке стороны и углы ромбов помечены и разрисованы (рис. 103), и тогда получается узор, заполняющий всю плоскость, как на рис. 4. Опять же «толстых» ромбов на замощение большой площади идет в 1,618 раз больше, чем «тонких», и N толстых / N тонких = φ. «Толстые» и «тонкие» ромбы теснейшим образом связаны со змеями и дротиками, а обе эти пары – посредством золотого сечения – с системой пятиугольника-пентаграммы.

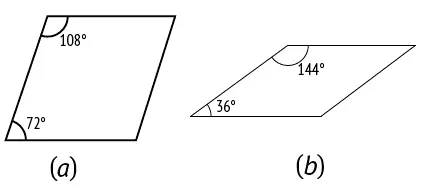
Рис. 101

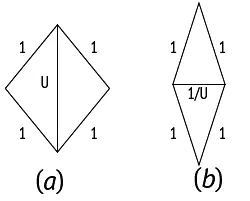
Рис. 102

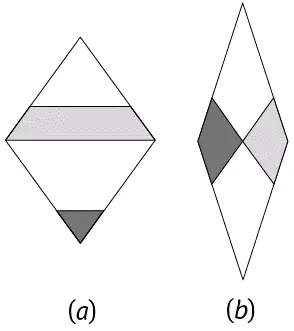
Рис. 103

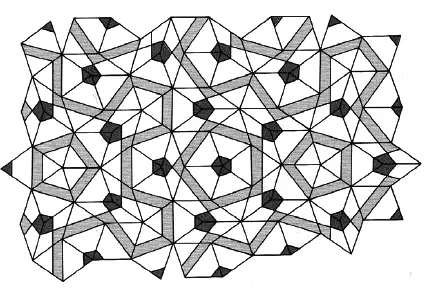
Рис. 104

Вспомним, что интерес пифагорейцев к золотому сечению начался с бесконечной череды вписанных друг в друга правильных пятиугольников и пентаграмм – как на рис. 105. На этом чертеже спрятаны все четыре плитки Пенроуза. Точки B и D отмечают противоположные дальние углы змея DCBA, а точки A и C – «крылышки» дротика EABC. Аналогичным образом можно найти на рисунке и «толстый» ромб AECD, и «тонкий» (в меньшем масштабе) ABCF.