Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Надеюсь, когда вам в следующий раз придется лакомиться ананасом, посылать любимой алую розу или любоваться на «Подсолнухи» Ван Гога, вы вспомните, что закон роста этих растений опирается на чудесное число, которое мы называем золотым сечением. Однако не забывайте, что рост растений зависит и от других факторов, а не только от оптимального расстояния между листьями. Следовательно, законы филлотаксиса, о которых я рассказал, нельзя считать такими же универсальными, как законы физики. Напротив, по словам знаменитого канадского математика Коксетера, это не более чем «на удивление сильная тенденция ».

Рис. 36

Однако ботаника – не единственная область в природе, где можно наткнуться на золотое сечение и числа Фибоначчи. Они проявляются в явлениях самого различного масштаба, от микроскопического до галактического. И их появление зачастую принимает обличье величественной спирали.

В истории математика не было семейства, породившего столько знаменитых математиков, сколько семья Бернулли: целых тринадцать!

Испугавшись «Испанской ярости» – кровопролитного восстания, поднятого в Нидерландах испанскими солдатами, – семейство бежало из Нидерландов, находившихся под властью испанских католиков, в Швейцарию, в город Базель. Три члена семьи, братья Якоб (1654–1705) и Иоганн (1667–1748) и второй сын Иоганна Даниил (1700–1782), были в интеллектуальном отношении на голову выше остальных родственников. Как ни странно, ожесточенные семейные распри прославили Бернулли чуть ли не в той же степени, что и многочисленные достижения в математике. Однажды Якоб с Иоганном повздорили особенно сильно. Началась ссора из-за разногласий по поводу решения знаменитой задачи по механике. Эта задача известна под названием «брахистохрона» (от греческих слов «брахистос», «кратчайший», и «хронос», «время») и состоит в том, чтобы найти кривую, по которой частица попадет из точки А в точку В под воздействием одной лишь силы гравитации за кратчайшее время. Братья независимо пришли к одному и тому же решению, однако в выкладках Якоба была ошибка, и он впоследствии пытался выдать выкладки Иоганна за свои. Печальным последствием этих событий стало то, что Иоганн стал профессором в Гронингене и до самой смерти брата ни разу не наведывался в Базель.

Связь Якоба Бернулли с золотым сечением прослеживается благодаря другой знаменитой кривой. Якоб написал трактат под названием « Spira Mirabilis » («Чудесная спираль») и посвятил ее особой разновидности спирали. Красота так называемой логарифмической спирали (рис. 37, названием она обязана тому, как радиус кривой возрастает по мере движения по часовой стрелке) настолько заворожила Якоба, что он завещал начертать эту фигуру и девиз, который он ей приписал – « Eadem mutate resurgo », «Измененная, вновь воскресаю прежней» – на своем надгробии.

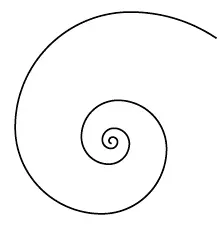
Рис. 37

Девиз отражает фундаментальное уникальное качество логарифмической кривой: с увеличением размера она не меняет формы. Эта черта называется самоподобием. Очарованный этим качеством, Якоб писал, что логарифмическую спираль «можно сделать символом как стойкости и постоянства в трудных обстоятельствах, так и человеческого организма, который после всех перемен, даже после смерти, восстанавливает точное свое подобие и полное совершенство».

Если немного подумать, станет ясно, что именно это свойство требуется для многих явлений роста и развития в природе. Например, по мере того как моллюск наутилус помпилиус (рис. 4) растет в своей раковине, он создает камеры все просторнее и просторнее, а те, которые стали ему малы, запечатывает. Каждая прибавка в длине раковины влечет за собой и пропорциональное увеличение радиуса, поэтому общая форма раковины остается неизменной. То есть «домик» у наутилуса всю жизнь одинаковый, и моллюску не приходится потом, например, сдвигать центр тяжести раковины. То же свойство присуще и бараньим рогам – они тоже имеют форму логарифмической спирали, хотя и не лежат в одной плоскости, – и изгибу слоновьих бивней. Логарифмическая спираль, набирая размер, становится шире, расстояние между «витками» увеличивается по мере отдаления от центра – так называемого полюса. Причем поворот на равные углы увеличивает расстояние от полюса на равные промежутки. Если бы мы, вооружившись микроскопом, увеличили бы витки, невидимые невооруженным глазом, до таких размеров, как на рис. 37, они в точности совпали бы с большой спиралью. Это свойство и отличает логарифмическую спираль от другой известной кривой, так называемой архимедовой спирали (в честь великого греческого математика Архимеда (ок. 287–212 гг. до н. э.), который подробно описал ее в своем трактате «О спиралях»). Архимедову спираль мы наблюдаем на торце рулонов туалетной бумаги или в рисунке каната, свернутого на полу. У спирали этого типа расстояние между витками всегда постоянно. К сожалению, каменщик, изготавливавший надгробие Якоба Бернулли, изобразил на нем по ошибке скорее архимедову, чем логарифмическую спираль, что, конечно, наверняка очень огорчило бы ученого.