Рудольф Сворень - Шаг за шагом. От детекторного приемника до супергетеродина

Когда грузик маятника находится в одном из крайних положений, его потенциальная энергия максимальна. По мере того как грузик опускается, его потенциальная энергия уменьшается, а кинетическая растет за счет увеличения скорости движения. Одним словом, при движении маятника к средней точке его потенциальная энергия переходит в кинетическую, и при прохождении средней точки потенциальная энергия маятника равна нулю, а кинетическая максимальна. Когда, проскочив по инерции среднюю точку, маятник двигается вверх, его кинетическая энергия постепенно переходит в потенциальную. Благодаря непрерывному переходу потенциальной энергии в кинетическую, а кинетической в потенциальную маятник совершает колебания — периодически отклоняется то в одну, то в другую сторону от своего среднего положения (рис. 39).

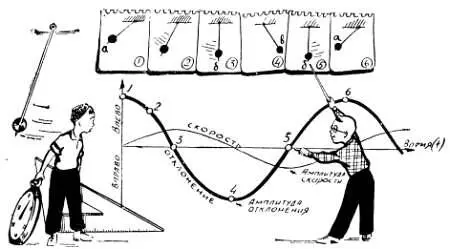
Рис. 39. В процессе колебаний маятника непрерывно происходит переход одного вида энергии в другой — потенциальная энергия (энергия поднятого маятника) периодически переходит в кинетическую (энергию движущегося маятника), кинетическая — обратно в потенциальную и т. д. При этом с определенной частотой меняется скорость движения маятника и его отклонение.

Аналогичными процессами сопровождаются и другие виды механических колебаний (лист 64).

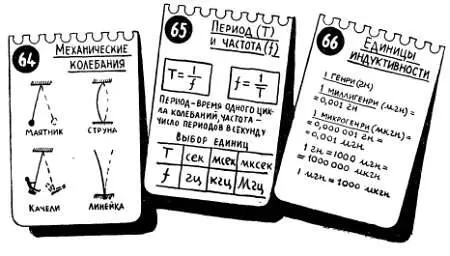
Попробуем записать все, что происходит с маятником в процессе его колебаний. Такую запись удобнее всего произвести с помощью особого рисунка — графика (рис. 40). Мы уже встречались с графиками в предыдущей главе.

Рис. 40. График — это очень удобный и наглядный способ записи зависимости одной величины от другой и, в частности, зависимости какой-либо величины от времени.

Основой графика являются две взаимно-перпендикулярные прямые линии, называемые осями. По горизонтальной оси мы будем в определенном масштабе отмечать время, для чего разметим эту линию-ось в единицах времени, подобно циферблату секундомера (рис. 40). По вертикальной оси, также в определенном масштабе, будем отмечать отклонение маятника от его среднего положения, и эту ось разметим в единицах длины.

Теперь будем через определенные промежутки времени (например, через каждую секунду) измерять отклонение маятника и делать соответствующие отметки-точки. При отклонении маятника вправо будем делать отметки вверх от нулевой точки, а при отклонении влево — вниз от этой точки. Такой выбор сделан совершенно условно: можно было бы принять и обратное направление. По отметкам-точкам, которые мы будем наносить па графике, можно будет построить кривую (так обычно называют линию, соединяющую отдельные точки графика), которая и расскажет о том, как перемещается маятник с течением времени. Из графика, например, можно увидеть, что колебания маятника постепенно ослабевают («затухают») — амплитуда [6] Как уже отмечалось ранее, амплитуда — это наибольшее (максимальное) значение какой-либо переменной величины. Рассматривая колебания маятника, мы отмечаем амплитуду скорости (когда грузик проходит точку б ), амплитуду отклонения (например, расстояние между точками а и б или б и в ), амплитуды потенциальной и кинетической энергии. Каждая из этих величин в течение одного периода дважды достигает амплитудного значений. отклонений становится все меньше и меньше (рис. 48), уменьшается и амплитудная (максимальная) скорость движения грузика. Колебания затухают потому, что энергия, запасенная при первом толчке, постепенно расходуется на преодоление сопротивления воздуха на трение в подшипнике или изгиб нити. Чем меньше эти потери энергии, тем медленнее затухают колебания.

Время, в течение которого маятник совершает полный цикл колебаний, называется периодом и обычно, подобно периоду переменного тока, обозначается буквой Т . Зная период, легко подсчитать частоту колебаний f и, наоборот, зная f , подсчитать Т :

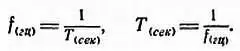
Так, например, если Т = 8 сек, то f = 0,125 гц, если колебания имеют частоту 100 гц, то период равен 0,01 сек (лист 65). Частота колебаний маятника, так же как и частота любых колебаний, зависит от того, насколько быстро в процессе этих колебаний энергия переходит из одного видав другой (в данном случае потенциальная энергия в кинетическую и обратно).