Б. Иванов - Осциллограф-ваш помощник (как работать с осциллографом)

Еще раз подчеркнем, что описанная методика измерений пригодна не только для магнитной антенны, а практически для любого колебательного контура.

И еще об одном варианте «индуктивных» измерений. Как известно, любая динамическая головка обладает своей резонансной частотой, которую необходимо знать при изготовлении громкоговорителя или акустической системы. Чтобы избежать ошибки, а также проконтролировать результат согласования динамической головки с акустическим объемом корпуса громкоговорителя, нужно предварительно более точно определить резонансную частоту головки. Здесь также поможет осциллограф, но в паре с генератором 3Ч, желательно с большой выходной мощностью (не менее 2 Вт). Соединяют их так, как показано на рис. 58, а .

Выходной сигнал генератора 3Ч поступает на цепочку из последовательно соединенных резистора R1 и динамической головки ВА1. Параллельно головке подключены входные щупы осциллографа, а «земляное» гнездо (или зажим) генератора соединено с гнездом « ВХОД X» осциллографа. Такое подключение осциллографа позволяет наблюдать фазовый сдвиг между током и напряжением в цепи звуковой катушки головки и фиксировать момент резонанса.

Сопротивление резистора R1 должно быть в 20…30 раз больше сопротивления звуковой катушки, чтобы амплитуда тока в цепи катушки оставалась постоянной — тогда наряду с фазой и частотой резонанса удастся определять амплитуду напряжения на катушке.

Последовательность работы напоминает вышеописанную процедуру измерения индуктивности катушек. Осциллограф работает в автоматическом режиме с разверткой от внешнего сигнала. Выходной сигнал генератора и чувствительность осциллографа устанавливают такими, чтобы при частоте генератора 200…500 Гц на экране осциллографа был виден эллипс (рис. 58, б ) с наклоном к линии развертки примерно в 45°.

Затем перестраивают частоту генератора в сторону нижних частот до получения прямой линии (рис. 58, в ). Получившаяся при этом частота генератора будет соответствовать резонансной частоте динамической головки.

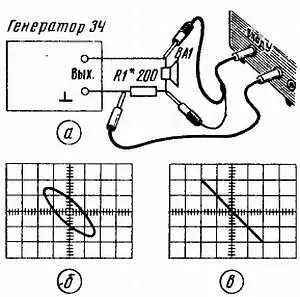
Рис. 58

Разве может о чем-то поведать импульс? — скажете вы. Импульс он и есть импульс, разве только прямоугольной формы. Но в том-то и дело, что если использовать прямоугольный импульс в качестве контрольного сигнала и подавать его, например, на вход усилителя 3Ч, то по форме выходного сигнала можно сразу же оценить работу усилителя и назвать его недостатки — малую полосу пропускания, недостаточное усиление на низших или высших частотах, самовозбуждение в какой-то области частот.

А возьмите широкополосный делитель напряжения, используемый, например, в самодельных измерительных приборах или осциллографах. «Пропущенный» через него прямоугольный импульс подскажет точные параметры деталей, необходимые для получения неизменного коэффициента деления сигнала в широком диапазоне частот.

Чтобы сказанное стало понятно, давайте сначала познакомимся с некоторыми параметрами импульсного сигнала, которые нередко упоминаются в описаниях различных генераторов, устройств автоматики и вычислительной техники. Для примера на рис. 59, а показан «внешний вид» несколько искаженного (по сравнению с прямоугольным) импульса, чтобы нагляднее были видны его отдельные части.

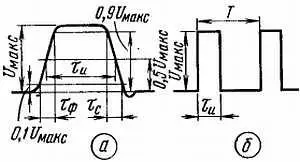
Рис. 59

Один из параметров импульса — его амплитуда ( U макс), наибольшая высота импульса без учета небольших выбросов. Продолжительность нарастания импульса характеризует длительность фронта τ ф, а убывания — длительность спада τ с. Продолжительность же «жизни» импульса определяет длительность τ и— время между началом и концом импульса, отсчитываемое обычно на уровне 0,5 амплитуды (иногда на уровне 0,7).

Вершина импульса может быть плоской, с завалом или подъемом. У прямоугольного импульса вершина плоская, а фронт и спад настолько крутые, что определить их длительность по осциллографу не удается.

Импульсный сигнал оценивают еще и скважностью, показывающей соотношение между длительностью импульса и периодом следования импульсов. Скважность — частное от деления периода на длительность. В показанном на рис. 59, б примере скважность равна 3.