Юрий Ревич - Занимательная микроэлектроника

А + В+ С= ( А+ В) + С= А+ ( В+ С) (ассоциативный закон сложения);

Ах А= А; А+ А= А;

А+ А¯ = 1; Ах А¯ = 0;

Аx 1 = А; А+ 1 = 1;

Аx 0 = 0; А+ 0 = А;

А + Ах В= А;

Ах ( В+ С) = Ах В+ Ах С;

А + Вх С= ( А+ В) х ( А+ В);

1¯ = 0; 0 = 1¯.

Булева алгебра на выключателях и реле

Для того чтобы представить булевы переменные и операции над ними с помощью технических устройств (то, что сделал Клод Шеннон в своей диссертации), надо придумать схемы, которые воспроизводили бы эти операции согласно вышеизложенным правилам. Самый простые варианты таких схем показаны на рис. 7.2.

Рис. 7.2. Схемы реализации логических функций на кнопочных выключателях

Здесь операции «И» и «ИЛИ» выполняются обычными кнопками без фиксации. Каждая из них соответствует одной логической переменной, которая принимает значение «1», если контакты замкнуты, и «О» — если разомкнуты. На выходе значению «О» соответствует погасший светодиод, «I» — горящий. Легко понять, что работать эти схемы будут именно так, как указано в правилах для соответствующих логических операций. Для технических устройств, которые, как мы увидим далее, могут выполнять функции, отличающиеся от базового набора булевых операций, правила соответствия входов и выхода называются «таблицами истинности» (или «таблицами состояния») и оформляются в следующем виде:

Если разобраться со схемами рис. 7.2 поглубже, то придется констатировать, что настоящими входными логическими переменными для них будут движения пальца, нажимающего на кнопку. В частности, операция «НЕ» здесь будет означать нажатие на кнопку с нормальнозамкнутыми контактами, а каскадное соединение таких схем для реализации сложных выражений предполагает наличие человека, транслирующего выходной сигнал одной схемы (состояние светодиода) во входной другой схемы (состояние контактов). Логично поставить вместо такого человека, «тупо» выполняющего предопределенные действия, техническое устройство. И здесь помогут уже хорошо нам известные электромагнитные реле.

В схемах на рис. 7.3 как для входов, так и для выхода наличие напряжения соответствует логической единице, отсутствие его — логическому нулю. (Можно для наглядности подключить к выходу светодиод или лампочку, но суть дела от этого не изменится.) Способ подачи входного сигнала не указан, т. к. предполагается, что источник входного напряжения может быть самый разный (разумеется, его мощность должна быть достаточной, чтобы заставить реле сработать) — в том числе и такая же схема на реле.

Рис. 7.3. Схемы реализации логических функций на реле

Последний вариант представлен на рис. 7.3 справа, где изображена схема составного элемента «И-НЕ» на трех реле, в виде совокупности элемента «И» (такого же, как на рисунке слева) и элемента «НЕ» (инвертора), который есть не что иное, как одиночное реле с выходом через нормальнозамкнутые, а не нормальноразомкнутые контакты. Таблица истинности для элемента «И-НЕ» будет выглядеть так:

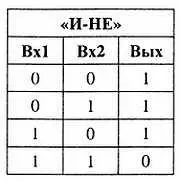
Легко видеть, что она не адекватна таблице для «ИЛИ», как могло бы показаться на первый взгляд. Аналогично составляется элемент «ИЛИ-HE» — из схемы «ИЛИ», показанной на рис. 7.3 посередине, и инвертора. Таблица истинности для него будет такой:

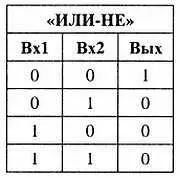
В большинстве современных серий логических микросхем используются именно элементы «И-НЕ» и «ИЛИ-HE», а не чистые «И» и «ИЛИ» (которые часто даже вовсе отсутствуют в составе некоторых серий, см. главу 8 ). Для того чтобы было проще разбираться в логических схемах, не заучивая таблицы истинности, работу элементов можно запомнить следующим образом: элемент «И» дает единицу на выходе только если на входах одновременно есть единица («оба одновременно»), элемент «ИЛИ» — если на любом из входов единица («хотя бы один»). Возможно, вам еще проще будет запомнить так: элемент «ИЛИ» дает единицу на выходе, если на входах «хотя бы одна единица», а элемент «И» дает ноль на выходе, если на входах «хотя бы один ноль». Рассмотренные же элементы с инверсией по выходу будут давать в тех же случаях обратные значения.