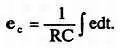В Бессонов - Радиоэлектроника для начинающих (и не только)

3.2.8. Сила тока отстает от напряжения на катушке индуктивности на угол π /2

Так как i= I mSin ωt , a u= U mSin ( ωt — π /2), то, следовательно, напряжение на катушке индуктивности опережает силу тока по фазе на угол π/2 . Это видно также на векторный (рис. 3.22, а ) и на временной (рис. 3.22, б ) диаграммах.

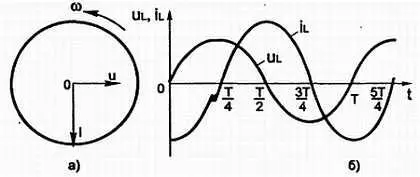
Рис. 3.22. Напряжение на катушке индуктивности опережает силу тока по фазе на угол 90°.

3.2.9. На активном сопротивлении (на резисторе) сила тока и напряжение совпадают по фазе

Так как i= I mSin ωt , и u= U mSin ωt , то, следовательно, напряжение на резисторе совпадает по фазе с силой тока . Это видно также на векторной (рис. 3.23, а ) и на временной (рис. 3.23, б ) диаграммах.

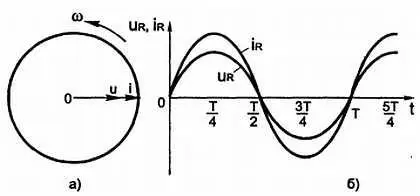
Рис. 3.23. Напряжение на резисторе совпадает по фазе с силой тока

В электронных устройствах часто бывает необходимо изменить прямоугольные импульсы или сигналы другой формы таким образом, чтобы получить сигнал требуемой формы. Указанное изменение может заключаться в сохранении высокочастотных составляющих сигнала и ослаблении низкочастотных составляющих, в ослаблении только высокочастотных составляющих, в изменении амплитуды и формы сигнала путем ограничения и т. д.

К таким устройствам можно отнести интегрирующую и дифференцирующую цепи, которые находят широкое применение в вычислительной технике, в системах развертки телевизионных приемников и в других случаях, когда необходимо ослабить высокочастотных составляющие импульсов.

Практически интегрирующую цепь (рис. 3.24, а .) можно рассматривать как фильтр нижних частот. При воздействии синусоидальных сигналов интегрирующая цепь сильнее ослабляет сигналы более высоких частот (и вносит некоторый фазовый сдвиг). В случае импульсных или прямоугольных сигналов их форма изменяется благодаря фильтрации высокочастотных сигналов.

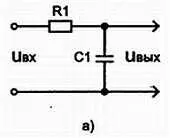
Рис. 3.24, а) Cxeма интегрирующей цепи

В практических схемах интегрирующих цепей постоянная времени t= RCвелика по сравнению с длительностью воздействующего импульса. В этом случае при ращение напряжения е сна конденсаторе мало по сравнению с напряжением е , приложенным к интегрирующей цепи. Тогда можно записать приближенное равенство:

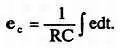
Таким образом, выходное напряжение интегрирующей цепи пропорционально интегралу входного тока e / R . Это можно объяснить, если обратиться к рис. 3.24, б и в .

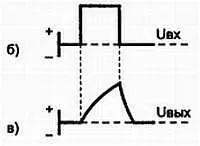
Рис. 3.24, б) форма входного импульса интегрирующей цепи, в) выходного импульса интегрирующей цепи

При подаче на вход схемы положительного импульса крутой фронт импульса действует на интегратор в течение очень короткого промежутка времени. Затем в течение времени, равного длительности импульса, действует напряжение, соответствующее плоской вершине импульса. Напряжение на конденсаторе нарастает по экспоненциальному закону. За время, равное постоянной времени цепи τ , напряжение на конденсаторе достигнет примерно 65 % максимального значения, а полностью конденсатор зарядится примерно в течение пяти постоянных времени (5 τ ). Так как постоянная времени интегрирующей цепи велика по сравнению с длительностью импульса, напряжение на конденсаторе не достигает максимального значения, а постепенно нарастает до некоторой величины (рис. 3.24, в ).

По окончании действия входного импульса конденсатор начнет разряжаться через резистор R1 и входную цепь. Разряд протекает медленно по сравнению со спадом входного импульса, и в результате на выходе формируется импульс, форма которого показана на рис. 3.24, в .

Если импульсы на входе интегратора имеют длительность, превышающую интервалы между ними (рис. 3.24, г ), то напряжение на конденсаторе будет постепенно нарастать.