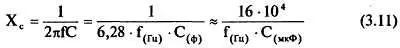В Бессонов - Радиоэлектроника для начинающих (и не только)

При замыкании выключателя SA (рис. 3.13, а ) лампочка кратковременно вспыхивает и гаснет. Это значит, что конденсатор не пропускает постоянный ток. Но из эксперимента можно сделать и другой вывод: в момент подключения батареи GB (замыкание выключателя SA ), когда напряжение на конденсаторе скачком увеличивается от нуля до 4,5 В, он не оказывает никакого сопротивления (т. е. его сопротивление в начальный момент равно нулю, все напряжение батареи приложено к лампе, сила тока максимальная). Со временем сила тока уменьшается и затем вовсе становится равной нулю. В этот момент конденсатор можно считать заряженным.

На рис. 3.13, б показан график зависимости силы тока, протекающего через конденсатор С и лампу накаливания EL , от времени, т. е. график заряда конденсатора. Из графика видно, что в момент замыкания выключателя SA (при t = 0) сила тока через лампу максимальная и равна I 0= E/ R л ~= 0,3 А.

Здесь R л= 14 Ом — сопротивление нити накала лампы.

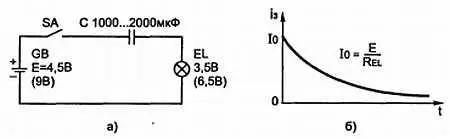
Рис. 3.13. а)Конденсатор не пропускает постоянный ток; б)График зависимости силы тока, протекающего через конденсатор Си через лампу накаливания EL

3.2.3. Сопротивление конденсатора переменному току зависит от его емкости и частоты тока

Меняя емкость конденсатора (рис. 3.14), можно убедиться, что лампа будет светиться по-разному. Для этого надо два конденсатора по 10 мкФ соединить параллельно, последовательно с ними включить лампочку EL на 3,6 В, на вход подать переменное напряжение 36 В. Зафиксировать яркость свечения лампочки. Затем подключить к этим конденсаторам параллельно еще один емкостью 5 мкФ и снова зафиксировать яркость свечения лампочки, — она увеличится. Отсюда вывод: с увеличением емкости конденсатора его сопротивление уменьшается. Обратите внимание, что все конденсаторы в этом эксперименте должны иметь рабочее напряжение не менее 60 В.

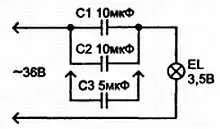
Рис. 3.14. Сопротивление конденсатора переменному току зависит от его ёмкости

Реактивное емкостное сопротивление конденсатора переменному току определяется по формуле:

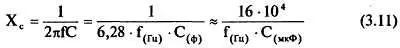
Тогда закон Ома запишется так:

I m= U m/ X c= 2 U mπ fC= U mω C. (3.12)

1 Ф = 10 6мкФ = 10 12пФ, 1 мкФ = 10 3нФ = 10 6пФ.

3.2.4.Сила тока опережает напряжение на емкости на угол π /2

Так как i= I mSin ωt , a u= U mSin ( ωt + π /2) то, следовательно, напряжение на конденсаторе отстает от силы тока по фазе на угол π/2 . Это видно на векторной (рис. 3.15, а ) и на временной (рис. 3.15, б ) диаграммах. Физически это можно понимать так: пока через конденсатор не потечет ток, на его пластинах не появятся заряды, до тех пор на пластинах и не будет напряжения.

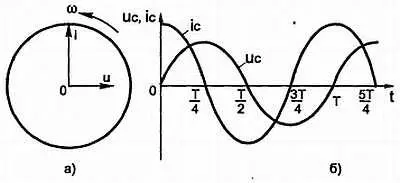
Рис. 3.15. Напряжение на конденсаторе отстаёт от силы тока по фазе на угод 90°

Мощность переменного тока будет равна: Р= I∙ Ucos φ . При φ = π /2 мощность Р = 0. Это значит, что конденсатор является реактивным элементом и не потребляет электрической энергии.

Если вы возьмете три конденсатора емкостью 1 мкФ каждый, соедините их параллельно, подключите в сеть 220 В и будете наблюдать за счетчиком электрической энергии, который имеется в вашей квартире, то счетчик никак не отреагирует на это подключение, хотя они по мощности эквивалентны лампочке мощностью 48 Вт. Почему счетчик не реагирует? Потому что конденсатор (как и катушка индуктивности) обладает замечательным свойством: в положительный полупериод напряжения сети он заряжается и накапливает электрическую энергию, а в отрицательный полупериод напряжения сети он отдает эту энергию снова в сеть. Это как морской прилив и отлив: то вода пригоняет к берегу все, что на ней плавает, то все смывает с берега, унося в море. Имейте в виду, что конденсатор должен быть рассчитан на напряжение 250…300 В.

Из графика на рис. 3.16 видно, что реактивное (емкостное) сопротивление конденсатора уменьшается как с увеличением емкости, так и с увеличением частоты питающего переменного напряжения; этот график построен по формуле (3.11). Аналогичными свойствами реактивного элемента обладает и катушка индуктивности.