В Бессонов - Радиоэлектроника для начинающих (и не только)

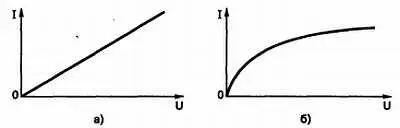
Рис. 3.9. ВАХ линейного элемента ( а) и нелинейного элемента ( б)

Внешний вид конденсаторов, их УГО и БЦО показаны на рис. 3.10.

Рис. 3.10. Внешний вид конденсаторов, их УГО и БЦО

Конденсатор, как и катушка индуктивности, оказывают переменному току сопротивление.

Последовательное и параллельное соединение конденсаторов.

Последовательное соединение конденсаторов (рис. 3.11, а ):

1/ С о= 1/ C1+ 1/ С2, (3.7, а )

отсюда:

С о= С1∙ С2/( С1+ С2) (3.7, б )

1/ С о= 1/ C1+ 1/ С2+ 1/ С3(3.8)

Параллельное соединение конденсаторов (рис. 3.11, б ):

С 0= С1+ С2, (3.9)

С 0= С1+ С2+ С3. (3.10)

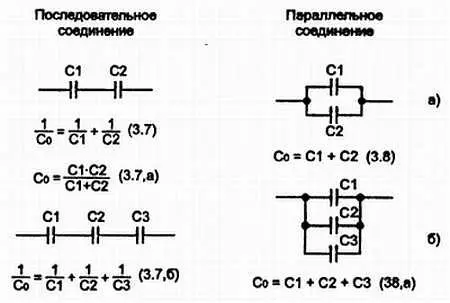
Ряс. 3.11. Последовательное ( а) и параллельное ( б) соединение конденсаторов

Обратите внимание: общая емкость при последовательном соединении конденсаторов вычисляется по формуле, аналогичной формуле для вычисления общего сопротивления при параллельном соединении резисторов, а общая емкость при параллельном соединении конденсаторов — по формуле, аналогичной формуле для вычисления общего сопротивления при последовательном соединении резисторов.

Для получения необходимой емкости при последовательном соединении конденсаторов требуются некоторые вычисления. Для облегчения подбора ёмкости второго конденсатора (при известном значении емкости первого) на рис. 2.22 ( глава 2 ) приведена номограмма.

Как пользоваться номограммой? При определении общих параметров деталей, номиналы которых имеют один порядок, пользуются шкалами ОА, ОВ, ОС , а если номиналы различаются на один порядок, то шкалами ОА, OD, ОЕ . Поясним это на примерах.

• Пример 1. Последовательно соединены конденсаторы емкостью 5 и 20 мкФ. Чему равна общая емкость? Приложив линейку к делению 5 на шкале ОА и к делению 20 на шкале OD , на шкале ОЕ прочтем результат — 4 мкФ.

• Пример 2 . Какой емкости конденсатор необходимо включить последовательно с конденсатором емкостью 5,6 пФ, чтобы их общая емкость была 2,5 пФ? Прикладывая линейку к делениям 5,6 на шкале ОА и 2,5 на шкале ОС , на шкале ОВ прочтем — 4,5 пФ.

Чтобы лучше понять принцип работы конденсатора и катушки индуктивности как реактивных элементов, рекомендуем вам самостоятельно провести ряд простых экспериментов.

3.2.1. Конденсатор как накопитель электрической энергии

Для этого соберите схему (рис. 3.12, а ). В положении переключателя SA, указанного на рисунке, конденсатор С будет заряжаться от батареи. Ток заряда протекает по цепи: «+» батареи GB резистор R —> переключатель SA —> конденсатор С —> «—» батареи GB. Через несколько секунд конденсатор зарядится и можно переключатель SA поставить в правое положение, лампочка кратковременно вспыхнет и погаснет. Чтобы лучше уяснить процесс заряда и разряда конденсатора, воспользуемся аналогией. Представим конденсатор в виде сосуда с крышкой, который может вместить определенное количество жидкости, например бензина.

После заполнения этого сосуда бензин можно вылить и поджечь, — это эквивалентно вспышке лампочки.

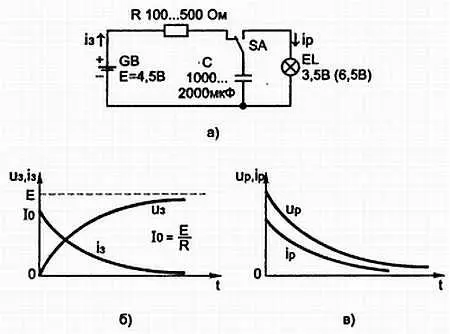
Рис. 3.12. а) Конденсатор — накопитель электрической энергии; б) График заряда конденсатора, в)график разряда конденсатора.

Для чего нужен резистор R в схеме рис. 3.12, а ? Если его не будет, то в момент подключения батареи к конденсатору ток заряда будет очень большим, конденсатор может взорваться от нагрева . Резистор R ограничивает ток заряда конденсатора. Конденсатор с хорошим диэлектриком может хранить заряд несколько суток; бумажные конденсаторы разряжаются почти полностью за несколько часов.

На рис. 3.12, б изображен график заряда конденсатора, а на рис. 3.12, в — график разряда конденсатора.

Емкость конденсаторов измеряется в фарадах (Ф), в микрофарадах (мкФ), нанофарадах (нФ), пикофарадах (пФ).

3.2.2. Конденсатор «не пропускает» постоянный ток