В Бессонов - Радиоэлектроника для начинающих (и не только)

Что мы под этим подразумеваем? Представим себе, что через спираль электрической плитки протекает синусоидальный ток и плитка каждую секунду выделяет количество теплоты Q . Теперь мы через некоторое время подключим эту же плитку в цепь постоянного тока и будем увеличивать напряжение до тех пор, пока плитка не будет выделять каждую секунду такое же количество теплоты, равное Q . В данном случае по своему тепловому действию оба напряжения (тока) равны. Поэтому сила постоянного тока (напряжения,), выделяющего в проводнике то же количество теплоты, что и данный переменный ток (напряжение), называется действующим значением переменного тока I (напряжения U ).

Для синусоидального тока действующее значение силы тока (рис. 3.8, а ):

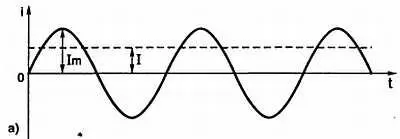
Рис. 3.8, а) действующее значение синусоидального тока;

I= I m/√2 = I m/1,414 = 0,707∙ I m(3.2, a )

Аналогично для напряжения и э.д.с.:

U= 0,707∙ U m(3.2, б )

Е= 0,707∙ Е m. (3.2, в )

Поэтому, когда мы говорим, что лампа накаливания рассчитана на 220 В, мы подразумеваем, что это действующее напряжение.

Аналогично, если мы лампочку от карманного фонаря, рассчитанную на напряжение 3,5 В, подключим к источнику переменного тока с напряжением 3,5 В, то накал нити лампочки будет таким же, как и при питании ее от батареи с напряжением на зажимах 3,5 В.

Из (3.2) видно: зная действующее значение силы тока I (напряжения U , э.д.с. Е ), которую можно измерить амперметром переменного тока, можно вычислить его амплитудное значение:

I m= I∙√2= 1,4141 (3.3, a )

U m= 1,414∙ U(3.3, б )

E m= 1,414∙ E(3.3, в )

Из формулы видно, что амплитудное значение синусоидального тока (напряжения, э.д.с.) почти в полтора раза (в 1,414 раза) больше его действующего значения. Так, амплитудное значение напряжения сети 220 В равно:

U m= U∙1,414 = 220∙1,414 = 311 В.

Все амперметры, вольтметры переменного тока калибруются на синусоидальном токе (напряжении); для переменного тока другой формы показания этих приборов нужно корректировать. Например, для переменного тока треугольной формы (рис. 3.8, б ) соотношение между действующим и амплитудным значениями определяется по формулам:

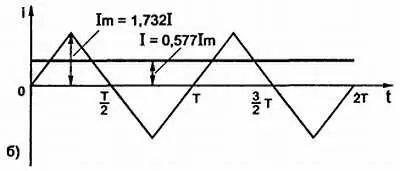
Рис. 3.8, б) соотношение между действующим и амплитудным значениями для переменного тока треугольной формы;

I= I m/√3 = 0,577∙ I m(3.4, a )

I m= 1,732∙ I(3.4, б )

Для последовательности прямоугольных импульсов (рис. 3.8, в ), называемых еще «меандром»:

I= I m(3.5)

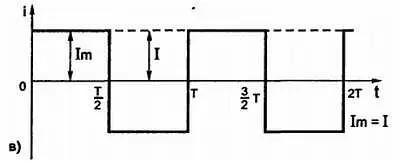
Рис. 3.8, в) соотношение между амплитудным и действующим значениями тока для последовательности прямоугольных импульсов;

а для последовательности коротких прямоугольных импульсов (рис. 3.8, г ):

I= I m∙√α (3.6)

где α= τ/ T, ( τ — длительность импульса).

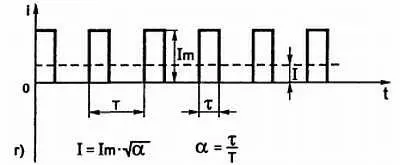
Рис. 3.8, г) Соотношение между амплитудным и действующим значениями для последовательности коротких прямоугольных импульсов

Элементами цепи переменного тока могут быть лампа накаливания, электрическая плитка, утюг, электродвигатель, резистор, конденсатор, катушка индуктивности, полупроводниковый диод, варистор и другие элементы. Лампа накаливания, электрическая плитка, утюг, резистор, диод, варистор представляют собой элементы, которые преобразуют электрическую энергию в тепловую. Говорят, что они обладают активным сопротивлением. А вот конденсатор и катушка индуктивности являются реактивными элементами , они не преобразуют электрическую энергию в тепловую, т. е. они не потребляют электрическую энергию, как, например, резистор, но обладают другими замечательными свойствами, которые будут рассмотрены ниже.

Кроме того, как указывалось в главе 2 , элементы цепи делятся на линейные и нелинейные. Линейные элементы имеют линейную ВАХ (вольт-амперную характеристику) (рис. 3.9, а ), нелинейные — нелинейную ВАХ (рис. 3.9, б ). Из перечисленных выше элементов линейными элементами являются резистор, конденсатор и катушка индуктивности, а остальные элементы нелинейные.