Карлос Касадо - Вселенная работает как часы. Лаплас. Небесная механика.

Из события «вытащен черный шар» следуют два возможных содержимых урны. Мы можем предположить, что оба варианта равновероятны (50% вероятности у каждого), однако применение теоремы Байеса увеличивает до 60 % вероятность того, что это первая урна, и снижает до 40 % вероятность того, что это вторая. Априори вероятности были равны (50 и 50%), а на основании наблюдений, апостериори, составили 60 и 40%. И это действительно так: поскольку первая урна содержит больше черных шаров, чем вторая, более вероятно, что шар был вытащен из первой урны.

Лапласу, как и Байесу, эта теорема позволила извлечь из опыта уроки и даже узаконить индукцию. Так, Лаплас вслед за графом де Бюффоном подсчитал вероятность того, что Солнце взойдет завтра, на основании количества дней подряд, когда оно уже восходило. Применяя теорему Байеса, Лаплас пришел к знаменитому «правилу последовательности».

«Для события, происходящего подряд п раз, вероятность того, что оно произойдет еще раз, равна (п + 1) / (п + 2).

Правило последовательности Лапласа

Эта теорема позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Вероятность события равна дроби, числитель которой является произведением вероятности события и вероятности связанного с ним события (причины), а знаменатель — суммой произведений вероятности события, учитывая каждую из причин, умноженную на вероятность каждой из причин. Эта формулировка, больше похожая на упражнение в дикции, имеет очень точное символическое выражение, которое можно найти в любом школьном учебнике:

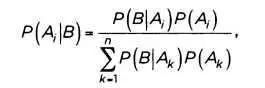
где Р(А iI B) — это апостериорная вероятность (то есть вероятность причины известного события), Р(В I А i) — вероятность события, причину которого предполагают, и Р(А i) — априорная вероятность (она предшествует любой информации о событии). Благодаря формуле Байеса априорные вероятности могут быть вычислены апостериори; иначе говоря, мы можем принимать решения, основываясь на опыте.

Если предположить, что Солнце встает каждое утро в течение 5 тысяч лет, то есть 1826213 дней (Лаплас именно таким полагал возраст Земли), то вероятность того, что оно встанет на следующий день, равна 1826214/1826215 (*99,9999%). Однако — на основании этого правила — чем дольше живет человек, тем больше вероятность того, что он продолжит жить. В 80 лет он будет иметь больше шансов прожить следующий день, чем в 20, а это абсурд. Байес, Лаплас и другие сторонники байесовской теории столкнулись со сложностью определения априорных вероятностей. В приведенном выше примере кажется справедливым предположить, что содержимое двух урн, в принципе, равновероятно, то есть составляет 50%. Но в некоторых ситуациях не всегда можно присвоить событиям одинаковую вероятность или рассчитать ее, исходя из имеющейся информации о каждом событии (субъективная вероятность). Можно ли определить вероятность объективно, например благодаря индукции определить ее как приблизительное значение частоты, опираясь на теорию Бернулли? Этот горячий научный спор, который вдохновил Лапласа, не завершен до сих пор: математики и философы и сегодня спорят о правильности различных подходов.

В 1780 году Лаплас представил «Мемуар о вероятностях», в котором усовершенствовал свой анализ этого вопроса. Ученый начал с того, что подчеркнул возможность определения вероятности тремя различными способами: априори, то есть посредством логических заключений; апостериори, то есть исходя из опыта; и третьим способом, очень близким к первому, который посредством умозаключений позволяет нам судить о степени вероятности будущего события. Первым способом мы можем установить равную вероятность при соперничестве между двумя игроками (каждый имеет 50 % шансов на победу). Благодаря второму способу мы можем определить вероятность выигрыша для каждого игрока исходя из результата предыдущих партий (если первый игрок выиграл семь партий из десяти, вероятность его выигрыша равна 70%). Наконец, при помощи третьего способа, если мы знаем, что первый игрок играет лучше второго, то можем предположить, что у него 80 % шансов на победу. В первом случае, говоря словами Лапласа, мы определили «абсолютную» вероятность (сегодня мы говорим «логическую вероятность»); во втором — «приблизительную» вероятность (объективную), а в третьем — «относительную» вероятность наших знаний и надежды. Также Лаплас определил различие между шансом и вероятностью. В его детерминистской философской концепции шанс по своей природе не имеет отношений к реальности. Учитывая, что все события имеют свои причины, шанс — это лишь выражение нашего незнания о причинах события. Вероятность — более подходящий способ описания нашего незнания причин, определяющих события.