Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Хага решил нарушить традиции. Что, если сложить угол на середину стороны? Не безумная ли идея?! Первый раз он сделал такое в 1978 году, и эта простая операция открыла двери в грандиозный новый мир. Хага получил три прямоугольных треугольника, но то были не просто прямоугольные треугольники. Все они оказались египетскими — самыми известными в истории и самыми каноническими треугольниками в мире.

Подстегиваемый трепетом сделанного открытия, он написал письмо о новом складывании профессору Коджи Фушими — физику-теоретику, известному своим интересом к оригами. «Я так и не получил ответа, — сказал Хага, — но затем он внезапно опубликовал статью в журнале „Mathematics Seminar“, ссылаясь там на теорему Хаги. Вот что получилось вместо ответа». С тех пор имя Хаги получили две другие «оригами-теоремы», а по его словам, у него таких еще с полсотни.

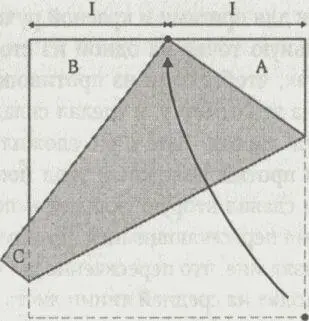
Теорема Хаги: треугольники А, В и С — египетские

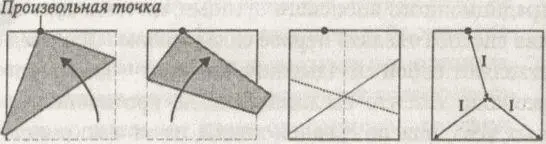
Другая теорема Хаги

В теореме Хаги угол складывается на середину стороны. Хага задался вопросом, возникнет ли что-нибудь интересное, если сложить угол на случайную точку на стороне. Решив это продемонстрировать мне, он взял синий квадратный листок из набора бумаги для оригами и красной ручкой отметил произвольную точку на одной из сторон, сложил листок так, чтобы один из противоположных углов попал на эту отметку, и сделал складку, а потом развернул листок. Затем он сложил его так, чтобы другой противоположный угол попал на ту же отметку, и сделал вторую складку, — получился квадрат с двумя пересекающимися линиями.

Хага показал мне, что пересечение двух складок всегда происходит на средней линии листа бумаги и что расстояние от выбранной произвольной точки до пересечения всегда равно расстоянию от пересечения до противолежащих углов. Меня это просто потрясло. Точка выбиралась случайным образом и вовсе не по центру. И тем не менее процесс складывания подобен самокорректируемому механизму!

Мне пришло в голову, что если про кого-то и можно сказать, что этот человек воплощает в современном мире душу Пифагора, то это определенно Кадзуо Хага. И у него, и у Пифагора одна и та же страсть к математическим открытиям, в основе которых — искреннее восхищение гармонией геометрии. И это восхищение, судя по всему, повлияло на Хагу в духовном плане аналогично тому, как это случилось с Пифагором две тысячи лет назад. «Большинство японцев пытаются в оригами создавать новые фигуры, — говорит Хага. — Моя же цель — уйти от идеи создания чего-то физического, а вместо этого открывать новые математические феномены. Вот почему я нахожу оригами таким интересным. Оказывается, в очень, очень простом мире все еще можно обнаружить захватывающие вещи».

Каждый год в расположенный на побережье индийский город Пури стекается миллион паломников. Собираются они ради самого зрелищного фестиваля в индуистском календаре — Рат Ятра («парад колесниц»), во время которого по городу проезжают три гигантские разукрашенные колесницы. Когда я туда приехал, улицы были заполнены любителями цимбал и мантр, босоногими святыми людьми с длинными бородами, а также индийскими туристами — типичными представителями среднего класса, одетыми в модные футболки и сари неоновых цветов. Была середина лета — начало сезона дождей, и, если не лил проливной дождь, работники фестиваля опрыскивали водой лица проходивших мимо, чтобы дать немного прохлады. Хоть и не столь масштабные, процессии фестиваля Рат Ятры проходят одновременно по всей Индии, но праздник в Пури — главное событие, а участвующие в нем колесницы — самые большие.

Фестиваль начинается по-настоящему, только когда местный святой — Шанкарачарья из Пури — предстает перед толпой и благословляет собравшихся. Шанкарачарья — один из самых важных индуистских мудрецов, глава монашеского ордена, корни которого уходят в историю более чем на тысячу лет. Из-за него-то я и отправился в Пури. Он — не только духовный лидер, но и публикующий свои работы математик.