Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

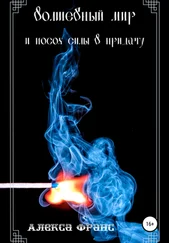
Прежде чем мы подойдем к губке Менгера, мне следует познакомить вас с ковром Серпинского. Эту замысловатую фигуру изобрел в 1916 году польский математик Вацлав Серпинский. Начнем с черного квадрата. Представим себе, что он сделан из девяти одинаковых подквадратиков, и удалим центральный (рис. А). Далее для каждого из оставшихся подквадратиков повторим эту операцию — то есть представим себе, что они сделаны из девяти подквадратиков каждый, и удалим центральные (рис. В). Снова повторим тот же процесс (рис. С). Ковер Серпинского — это то, что получится, если продолжать подобные действия до бесконечности.

В 1926 году австрийский математик Карл Менгер предложил трехмерный вариант ковра Серпинского, получивший известность как губка Менгера. Начнем с куба. Представим себе, что он сделан из 27 одинаковых подкубов, и удалим подкуб, расположенный в самом центре, а заодно и шесть подкубов в центре каждой грани исходного куба. Получается куб, в котором просверлили три квадратные дырки (рис. D). Поступим с каждым из оставшихся 20 подкубов как с исходным кубом и удалим 7 из 27 подкубов из каждого (рис. E). Повторим этот процесс еще раз (рис. F), после чего наш куб примет такой вид, будто в нем пировал целый выводок геометрически озабоченных древесных червей.

Губка Менгера

Губка Менгера — поразительный, парадоксальный объект. При продолжении итераций, в ходе которых удаляются все меньшие и меньшие кубы, объем губки все уменьшается, и в конце концов она становится невидимой — как если бы древесные черви съели ее целиком. Однако при каждой итерации, состоящей в удалении кубиков, площадь поверхности губки возрастает. Совершая все больше и больше итераций, можно сделать площадь его поверхности больше любого наперед заданного значения, а это означает, что, когда число итераций стремится к бесконечности, площадь поверхности губки также стремится к бесконечности. В пределе губка Менгера — это объект с бесконечно большой площадью поверхности, но при этом невидимый.

Мозли построила губку Менгера третьего уровня — другими словами, губку, получаемую за три итерации удаления кубиков (рис. F). На это у нее ушло десять лет. Она прибегла к помощи около 200 человек и использовала 66 048 карточек. Построенная ею губка имеет высоту, ширину и глубину по четыре фута и восемь дюймов.

«Я долгое время размышляла над вопросом, делаю ли я нечто совершенно нелепое, — сказала она мне. — Но когда я закончила работу и взглянула на эту штуку, я осознала, что ее масштаб придал всему делу великолепие. Особенно чудесно, что в модель можно засунуть голову и плечи и посмотреть на эту изумительную фигуру с такой точки зрения, с которой раньше никто на нее не смотрел. Это было бесконечно пленительно, потому что чем глубже в нее погружаешься, тем больше видишь повторяющих самих себя структур. Просто смотришь на все это, и ничего объяснять не требуется. Это идея, воплощенная в материале; математика, ставшая наглядной».

Хотя оригами — исходно японское изобретение, приемы складывания бумаги развивались — причем совершенно независимо — и в других странах. В Европе пионером оригами был немецкий преподаватель Фридрих Фрёбель, в середине XIX столетия использовавший складывание объектов из бумаги как метод обучения маленьких детишек началам геометрии. Оригами обладало тем преимуществом, что позволяло его подопечным в детском садике наблюдать за тем, как геометрические объекты создаются в пространстве, а не просто рассматривать их плоские изображения на рисунках. Пример Фрёбеля перенял другой математик — индиец Сундара Роу, написавший в 1901 году книгу «Геометрические упражнения со складыванием бумаги», в которой он утверждал, что оригами — математический метод, в ряде случаев оказывающийся более мощным, чем Евклидов. Он говорил, что «несколько важных геометрических процессов можно осуществить намного проще, чем с циркулем и линейкой». Но даже Роу не мог предвидеть, насколько это мощный метод — оригами.

В 1936 году итальянка Маргерита Пьяццола Белок из Университета Феррары опубликовала статью, где доказала, что, взяв лист бумаги с отмеченной на нем длиной L, можно сложить его так, чтобы получить длину, равную кубическому корню из L. Может быть, тогда она этого и не осознавала, но из ее утверждения следовало, что с помощью оригами решалась задача, поставленная перед афинянами делосским оракулом, когда он потребовал, чтобы афиняне удвоили объем куба. Делосская задача переформулируется как задача построения куба со стороной в кубический корень из двух — раз большей стороны заданного куба. 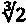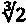С использованием оригами задача сводилась к складыванию длины , исходя из длины 1. Поскольку мы можем удвоить 1 и получить 2 путем складывания 1 самой на себя, а кроме того, можем найти кубический корень из 2, следуя предписанию Белок, значит, задача решена. Из доказательства Белок также следовало, что любой угол можно разделить на три равные части — и тем самым была побеждена вторая великая нерешаемая задача Античности. Статья Белок, однако, пребывала в безвестности десятилетия, пока в 1970-х годах математики не занялись оригами всерьез.