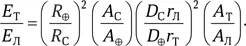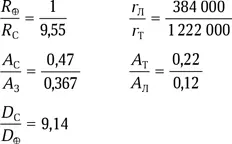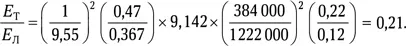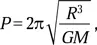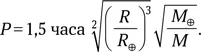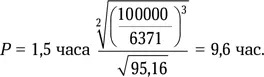Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

Мы видим пепельный свет Луны, потому что сами находимся на источнике освещения, т. е. на Земле (см. задачу «Пепельный свет» в разделе «Прогулка по Земле»). Именно поэтому солнечный свет, отраженный Землей, полностью освещает ту часть темной стороны Луны, которая в данный момент видна с Земли. Фото Титана сделано космическим зондом «Кассини» (NASA) не со стороны Сатурна, поэтому не видно пепельного света.

Мы можем оценить ожидаемую яркость пепельного света Титана (Т) по сравнению с пепельным светом Луны (Л), сравнивая потоки солнечного света ( I ) у Земли (⊕) и Сатурна (С), видимый со спутника диаметр планеты ( D ) и альбедо ( A ) планеты и спутника. Для этого мы используем расстояния планет от Солнца ( R ) и спутников от планет ( r ). Итак, отношение яркостей пепельного света ( E ) составит:

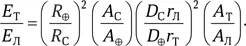
В астрономических справочниках мы легко найдем значения этих величин и вычислим их отношения.

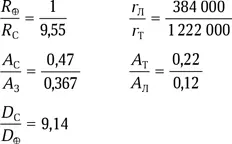
А теперь можно вычислить отношение

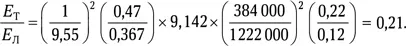
Как видим, ожидаемая яркость пепельного света Титана почти в 5 раз меньше лунного. Какие же факторы играют в этом основную роль? Удаленность Сатурна от Солнца почти полностью компенсируется его большим собственным размером. Альбедо Сатурна и Титана больше, чем Земли и Луны, что дает преимущество Титану. Но главную роль в слабости его пепельного света играет относительная удаленность Титана от Сатурна. Тем не менее на фоне космической темноты пепельный свет Титана должен быть виден. Надо лишь поймать удобный ракурс — сфотографировать Титан со стороны Сатурна в фазе, близкой к «новолунию».

Ослабление света на 1 m, т. е. примерно в 2,5 раза, говорит о том, что не менее половины проходящих сквозь кольцо фотонов поглощается или рассеивается в нем. А значит, и твердые частицы самого кольца, пересекая его по толщине (из-за небольшого различия в наклонах орбитальных плоскостей), имеют шанс не менее 50 % столкнуться с другими частицами. Двух пересечений достаточно, чтобы считать этот шанс близким к 100 %. За один орбитальный оборот частица как раз испытывает два пересечения, если не движется точно в центральной плоскости кольца. А если и движется в центральной плоскости, то все равно имеет не меньший шанс столкнуться с теми частицами, которые пересекают эту плоскость.

Орбитальный период ( P ) частиц в разных областях кольца разный в зависимости от расстояния ( R ) до центра планеты:

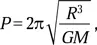
где M — масса Сатурна. Для упрощения вычислений выразим M и R через массу и радиус Земли (⊕), чтобы использовать известный нам орбитальный период на низкой околоземной (гагаринской!) орбите:

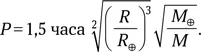
Масса Сатурна равна 95,16 M ⊕, а радиус наиболее плотной части ярчайшего кольца B — около 100 000 км. Следовательно, орбитальный период частиц в нем равен

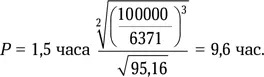
Это и есть характерное время между столкновениями частиц. За один орбитальный оборот частица дважды пересекает кольцо по толщине ( L ). Поэтому характерная скорость взаимного столкновения частиц V ≈ 2 L / P . Толщина колец Сатурна оценивается от 10 м до 1 км. Примем L = 100 м, тогда V≈ 200 м / 9,6 час = 6 мм/с. Столь мягкие касания скорее могут привести к слипанию частиц, чем к их разрушению.

Для оценки блеска звездолета используем простейший метод — сравним его с Луной, полагая, что звездолет обращается вокруг Земли. Пусть А Зи А Л— альбедо звездолета и Луны, L Ли D Л— расстояние до Луны и ее диаметр, L Зи D З— расстояние и средний диаметр звездолета. Тогда при их одинаковом освещении Солнцем отношение потоков света от них у поверхности Земли составит ( А З/ А Л)( D З L Л /D Л L З) 2. Пусть видимая поверхность обоих полностью освещена Солнцем. При этом Луна в фазе полнолуния, а значит, ее звездная величина, как известно, составляет –12,7 m. Тогда звездная величина звездолета составит