Пусть F — сила притяжения тела к Земле. Вес — это сила, с которой тело давит на опору. С такой же по величине силой опора давит на тело (третий закон Ньютона). Обозначим эту силу через F 1. Вместе с ракетой тело движется вверх с ускорением g , и, следовательно, сумма F 2всех действующих на него сил равна mg (второй закон Ньютона). Положительным направлением мы выбрали направление движения ракеты, т. е. вверх. Поскольку
F 2= F + F 1,
получим
F 1= F 2− F ,
где F 2= mg и F = − mg . Отсюда F 1= 2 mg . Таким образом, у поверхности Земли вес тела равен 2 mg . С удалением от Земли сила притяжения F уменьшается, приближаясь к нулю (закон тяготения Ньютона). В предельном случае при F = 0 и F 1= F 2вес тела будет равен mg . Итак, вес тела убывает от 2 mg у поверхности Земли до mg на бесконечности.
3.20. Из пушки на Луну — 1
Если при выстреле сообщить аппарату достаточно большую скорость, такую, чтобы, выйдя за пределы земной атмосферы, он двигался со скоростью больше второй космической, то при правильном выборе направления выстрела аппарат будет двигаться по кеплеровской орбите и сможет достигнуть Луны, Марса, Солнца. Но спутником Земли он не станет. Ведь в этом случае, двигаясь по эллипсу вокруг Земли и завершая первый оборот, аппарат должен будет пройти через точку старта, что непременно приведет к его столкновению с Землей или по крайней мере с ее атмосферой.
Поэтому просто из пушки запустить ИСЗ нельзя. Однако идея наземного ускорителя («пушки») для запуска ИСЗ все же не отброшена. Подумайте, при каких условиях она может быть реализована.
3.21. Из пушки на Луну — 2
Для достижения скорости V = 11 км/с, необходимой при старте к Луне, двигаясь с ускорением а , нужно пройти путь
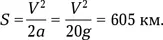
Такую глубокую шахту создать невозможно. Вес человека в момент выстрела увеличился бы в 11 раз (см. задачу 3.17 «Взлетаем»). Для человека это предельная перегрузка. Однако приборы спутников могут выдерживать ускорение до 10 4 g . При этом длина пушки сокращается до 1 км, что технически вполне осуществимо.
Из формулы для центростремительного ускорения ( a = v 2/ r ) найдем значение 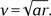 Тогда для a = g получим
Тогда для a = g получим 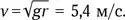 Это нормальная скорость бега для тренированного человека. Ориентация станции в данном случае никакого значения не имеет.
Это нормальная скорость бега для тренированного человека. Ориентация станции в данном случае никакого значения не имеет.
Нет, не смогут. Вездеход должен двигаться со скоростью не больше первой космической ( V I), иначе он оторвется от поверхности и потеряет опору. Найдем время облета астероида по низкой орбите с этой предельной скоростью:
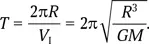
Учтем, что плотность астероида выражается так:
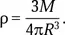
Тогда
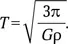
Это очень важная формула. Она показывает, что время оборота по низкой орбите зависит не от размера притягивающего тела, а только от его средней плотности.
Для поиска численных значений удобно помнить, что у низколетящего спутника Земли Т = 1,5 часа, а плотность Земли ρ ⊕= 5,5 г/см 3. Тогда для планеты плотности ρ получим: Т = 1,5 час 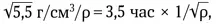 если плотность измеряется в граммах на 1 см 3.
если плотность измеряется в граммах на 1 см 3.
Зная плотность астероида, определим 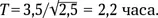 Значит, вездеход не сможет объехать астероид за 2 часа. За такое время его нельзя облететь даже на ракете с выключенными двигателями. А с включенными? См. задачу 3.25 «Спасти космонавтов».
Значит, вездеход не сможет объехать астероид за 2 часа. За такое время его нельзя облететь даже на ракете с выключенными двигателями. А с включенными? См. задачу 3.25 «Спасти космонавтов».
Читать дальше
Конец ознакомительного отрывка
Купить книгу

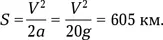
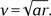 Тогда для a = g получим
Тогда для a = g получим 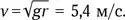 Это нормальная скорость бега для тренированного человека. Ориентация станции в данном случае никакого значения не имеет.
Это нормальная скорость бега для тренированного человека. Ориентация станции в данном случае никакого значения не имеет.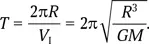
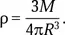
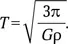
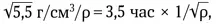 если плотность измеряется в граммах на 1 см 3.
если плотность измеряется в граммах на 1 см 3.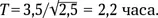 Значит, вездеход не сможет объехать астероид за 2 часа. За такое время его нельзя облететь даже на ракете с выключенными двигателями. А с включенными? См. задачу 3.25 «Спасти космонавтов».
Значит, вездеход не сможет объехать астероид за 2 часа. За такое время его нельзя облететь даже на ракете с выключенными двигателями. А с включенными? См. задачу 3.25 «Спасти космонавтов».










