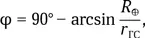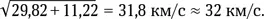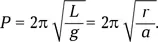
Значит, период колебания снаряда в шахте (независимо от амплитуды колебания!) составит
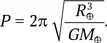
А полет между полюсами будет длиться
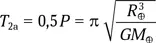
Таким образом, в случае однородной Земли снаряды прибудут к Южному полюсу одновременно ( Т 1= Т 2a).
Однако известно, что к центру Земли плотность увеличивается, поэтому рассмотрим другой крайний случай.
б) Пусть вся масса Земли сосредоточена в ее центре. Тогда ускорение снаряда
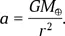
Это уравнение движения в поле точечной массы, типичное для тел Солнечной системы. Движение нашего снаряда по радиальной орбите можно представить как движение по вырожденному эллипсу с эксцентриситетом, практически равным единице. Тогда большая полуось этого эллипса равна R ⊕/2, а орбитальный период
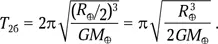
Это в 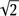 раз меньше, чем Т 1или Т 2a. Очевидно, что истинное значение времени полета снаряда через шахту ( Т 2) удовлетворяет неравенству Т 2a> Т 2> Т 2б. Следовательно, Т 2< Т 1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!).
раз меньше, чем Т 1или Т 2a. Очевидно, что истинное значение времени полета снаряда через шахту ( Т 2) удовлетворяет неравенству Т 2a> Т 2> Т 2б. Следовательно, Т 2< Т 1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!).
Задача решена. А теперь попробуйте рассмотреть третий вариант распределения плотности Земли — совершенно невероятный: пусть вся масса планеты сосредоточена в ее бесконечно тонкой оболочке, а внутри — пусто. Желаю успеха!
3.14. К антиподам разными путями
На снаряд, движущийся в плоскости экватора, будет (в системе отсчета, связанной с Землей) действовать центробежная сила, ослабляющая силу тяготения. Поэтому он пройдет через центр Земли позже и не столкнется с полярным снарядом, а на путь к антиподам затратит большее время. Полярный снаряд его опередит.
3.15. Связь между полюсами
Максимальную широту, на которой геостационарные спутники еще видны над горизонтом, определим из условия видимости объекта на горизонте
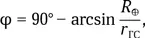
где r ГС= 42 166 км — радиус орбиты геостационарного спутника. Приняв Землю за шар и взяв R ⊕= 6371 км, получим φ = 90° — 8,7° ≈ 81°. На более высоких широтах и тем более на полюсах Земли геостационарные спутники не видны с уровня моря. Значит, и связь с их помощью невозможна.
Кроме очевидного решения (южный полюс) существует еще бесконечное число таких точек в районе северного полюса, на расстоянии от него (35 + 20/2π n ) км, при n = 1, 2, …
Автор ошибочно привел значение скорости на низкой околоземной орбите, тогда как для Марса значение этой скорости существенно меньше — всего около 12 800 км/ч.
Простейшее решение — после разрыва гравитационной связи с Землей развить скорость ее орбитального движения (около 30 км/с) в сторону, противоположную этому движению, т. е. «остановиться» на орбите и начать падать на Солнце по радиусу-вектору. Для этого вблизи Земли с учетом ее притяжения ракете необходимо развить скорость (мы помним, что сумма кинетических энергий — это сумма квадратов скоростей)
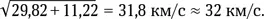
Заметим, что до такой скорости еще ни одна ракета не разгонялась. Поэтому более разумное решение — использовать для изменения скорости ракеты притяжение какой-либо планеты, совершив вблизи нее пертурбационный (гравитационный) маневр. Например, направив ракету к Юпитеру со скоростью около 16 км/с, можно таким образом рассчитать ее движение, что, сблизившись с планетой-гигантом, она изменит траекторию и упадет на Солнце. К сожалению, притяжения Марса для этого недостаточно.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

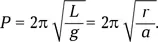
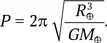
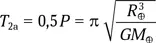
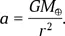
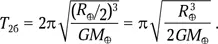
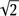 раз меньше, чем Т 1или Т 2a. Очевидно, что истинное значение времени полета снаряда через шахту ( Т 2) удовлетворяет неравенству Т 2a> Т 2> Т 2б. Следовательно, Т 2< Т 1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!).
раз меньше, чем Т 1или Т 2a. Очевидно, что истинное значение времени полета снаряда через шахту ( Т 2) удовлетворяет неравенству Т 2a> Т 2> Т 2б. Следовательно, Т 2< Т 1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!).