Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

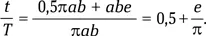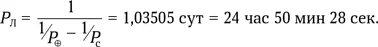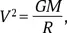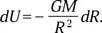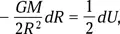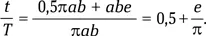
При e → 1 получим t/T = 0,5 + 1/π = 0,81831…

Для T = 90 мин получим t = 74 мин, а вовсе не 45 мин, как думают некоторые! (См. статью А. Кларка «Введение» в книге «Исследование мирового пространства», М.: Физматгиз, 1959, с. 9.)

Положение Луны относительно космодрома повторится через «лунные сутки» ( P Л), равные периоду обращения Луны относительно поверхности Земли. Период обращения Луны вокруг центра Земли (сидерический месяц) равен P c= 27,321662 сут, период вращения Земли равен P ⊕= 23 час 56 мин 04 сек = 23,934469 час = 0,9972696 сут. Поскольку орбита Луны не круговая, можно говорить лишь о средних лунных сутках, которые равны

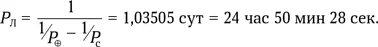
Таким образом, на следующие сутки Луна окажется примерно в том же положении на небе относительно небесного меридиана космодрома на 50,5 минут позже. Учитывая неравномерность движения Луны, можно сказать, что через сутки Луна «запаздывает» примерно на 1 час. Действительно, 9 сентября 1959 г. старт к Луне был назначен на 6 час 39 мин 50 сек. Однако он тоже не состоялся. Следующая (успешная!) попытка состоялась 12 сентября в 9 час 39 мин 26 сек.

Глядя на назначенные моменты старта, легко догадаться, в какой части своей орбиты была Луна. В среднем Земля «догоняет» ее 50,5 мин, а в те дни ей каждый раз требовался без малого час. Следовательно, Луна двигалась быстрее среднего, значит, была в районе перигея своей орбиты. Заглянув в астрономический календарь или электронный планетарий, мы увидим, что это действительно так!

Трение о разреженные верхние слои атмосферы действительно стало причиной падения первого спутника (как и многих других после него). Однако, приближаясь к Земле, спутник не терял скорость движения, а напротив — увеличивал ее. Это один из «парадоксов» космонавтики (см. Штернфельд, 1991). Какой бы эллиптичной орбита спутника ни была вначале, в результате трения об атмосферу она округляется, поскольку максимальное трение наблюдается в области перигея. А для скорости движения по круговой орбите справедлива формула, определяющая первую космическую скорость:

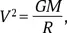
где G — гравитационная постоянная, M — масса Земли, R — радиус орбиты. Если R уменьшается, то V возрастает. Казалось бы, парадокс: трение приводит к росту скорости! Но ясно, что к росту скорости приводит не трение, а гравитация: работа силы тяжести ускоряет движение спутника и компенсирует потерю энергии на трение. При этом работа силы тяжести делится ровно пополам: половина идет на рост кинетической энергии спутника (т. е. скорости), а вторая половина уходит в тепло из-за трения.

Действительно, гравитационная энергия на единицу массы спутника равна GM/R , а ее изменение при небольшом сокращении радиуса орбиты составляет

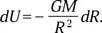
При этом удельная кинетическая энергия ( V 2/2) возрастает на

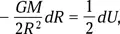
а вторая половина dU рассеивается через трение в тепло. Это частный случай теоремы вириала.

Скорость спутника возрастает до той поры, пока он не проник в плотные слои атмосферы. Начиная с некоторой высоты, гравитация уже не в состоянии компенсировать потерю энергии на сопротивление воздуха, и спутник начинает замедляться, а если он недостаточно прочный, то и разрушаться. Конкретное значение этой высоты зависит от массы и размера спутника. Обычно оно лежит в интервале 70–90 км.

Одновременный запуск двух ракет с одного космодрома невозможен по техническим причинам: при подготовке запуска и в первые минуты полета каждой ракеты задействованы все службы контроля космодрома. А следующая возможность запустить ракету на орбиту так, чтобы она оказалась недалеко от первой, представляется в тот момент, когда запущенная первой завершает свой первый виток вокруг Земли и пролетает сравнительно недалеко от космодрома. На низкой околоземной орбите один облет Земли длится как раз 1,5 часа.

Кроме того, эта задержка во времени дает возможность точно определить параметры орбиты первой ракеты и точнее нацелить к ней вторую ракету. Разумеется, за 1,5 часа из-за вращения Земли космодром переместится от точки первого старта. Поскольку речь идет о космодроме на мысе Канаверал (Флорида, США), расположенном на 28,5° с. ш., то это смещение составит