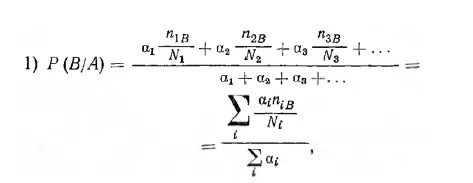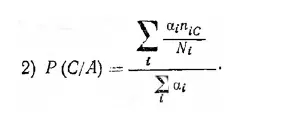Вячеслав Иванников - Культурно-историческая психология волевого действия - От прогноза – к поступку

В величину вероятностного прогноза события В при условии, что непосредственно перед тем было А, входят: доля карточек В среди первых N 1 карточек в ящике А с коэффициентом а 1, доля карточек В среди следующих N 2 карточек в ящике А с коэффициентом а 2, доля карточек В среди следующих N 3 карточек в ящике А с коэффициентом а 3 и т. д. Вероятность того, что наступит событие В при условии, что произошло событие А, будет такой:

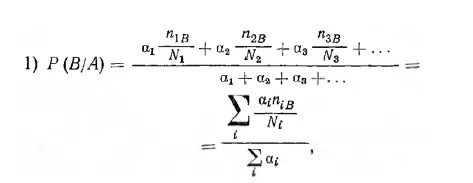
где а 1>а 2>а 3 ….

Это и есть вероятность, с которой прогнозируется наступление события В в случае, если произошло А. Точно так же для любого другого события С:

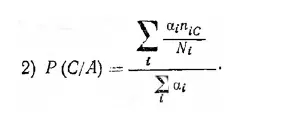
При такой организации памяти моделируется уже не только вероятностное прогнозирование и, в частности, классический условный рефлекс; но и еще одно интересное явление, которое наблюдается в опытах по переделке условных рефлексов.

Пусть собака в определенных условиях после звонка всегда (в течение достаточно долгого времени) получала пищу. В результате в этих условиях после звонка у собаки начинается усиленное выделение слюны – результат того, что попадание пищи в рот прогнозируется с большой вероятностью. Однако в очередной раз после звонка собака не получила пищу, а последовало болевое раздражение лапы. То же повторилось в следующий раз после звонка – и еще несколько раз. Теперь уже в ответ на звонок собака отдергивает лапу, а усиления слюноотделения не наблюдается. Собака ведет себя так, как будто она «забыла», что ее кормили после звонка, но «помнит», что после звонка было больно лапе. Однако опыт показывает, что собака ничего не «забыла». Если оставить такую собаку на достаточно длительное время в покое (не кормить после звонка и не пользоваться током), а затем привести в лабораторию и включить звонок, у нее может возникнуть усиленное слюноотделение. Собака как бы «вспомнила», что ее когда-то кормили после звонка, и как бы «забыла» более недавние события – болевое раздражение после звонка.

Похожие явления можно наблюдать и у человека. В квартире во время ремонта перенесли выключатель – он был слева от двери, а стал справа. Первое время хозяин, заходя в квартиру, по привычке шел в темноте налево. Но через небольшое время он переучивается и идет уже к выключателю направо. Но если в это время хозяин уедет на месяц, то, вернувшись, он может снова начать искать выключатель на левой стороне, как говорят, «по старой памяти». Человек как бы «забыл» более недавний кратковременный опыт и как бы «вспомнил» ранее «забытый», более старый, но долговременный опыт.

Такое «забывание» старого при изменении среды и «вспоминание» после перерыва обеспечивается в модели с «весовым коэффициентом давности». Недавние события могут «перевешивать» даже длительный, но более старый опыт, благодаря высокому «весовому коэффициенту давности» (площадь S 2 на рисунке 1 больше площади S 1). По прошествии длительного времени, когда «весовой коэффициент давности» тех же событий уменьшится, опыт этого короткого периода уже не доминирует над длительным опытом (площадь S 2 меньше площади S 1). Но если теперь вновь восстановить такие же вероятностные характеристики среды, как в период t 1t 2, то обучение уже пойдет быстрее, чем в первый раз: площадь S 3 суммируется с площадью S" 2; поэтому время повторного обучения t 3t 4 окажется меньше времени первичного обучения t 1t 2. Повторное обучение требует тем меньшего времени, чем быстрее оно проводится после первичного обучения и чем длительнее было первичное обучение.

В модели, как она описана выше, вероятностное прогнозирование осуществляется по отношению к одному событию, предшествующему прогнозируемому событию. Ясно, однако, что такой прогноз не может быть достаточно надежным в среде, в которой имеются связи между событиями не только рядом стоящими, но и более отдаленными (марковские последовательности [2] Марковской (по имени математика А. А. Маркова) называют такую случайную последовательность, составленную из элементов А, В…, К, в которой имеется зависимость между элементами. Эта зависимость выражается в том, что элемент D определяет вероятность P(E/D) того, что следующим в последовательности будет Е. Величина P ( E / D ) называется переходной вероятностью или условной вероятностью того, что при условии появления элемента (или возникновения события) D последует Е. с «глубиной марковости» 2 и больше). Так, например, событие D может следовать с высокой вероятностью за событием В, если перед В было А, и с низкой вероятностью, если перед В было С. В описанной выше модели прогноз вероятности наступления события D после В осуществляется без учета того, какое событие предшествовало В – в ящике В не содержится информации о том, что предшествовало событию В.