Роб Истуэй - Математика для мам и пап - Домашка без мучений

142 – 8 =

142 – 2 = 140 и 140 – 6 = 134.

Второй метод называется компенсацией:вы прибавляете или вычитаете больше или меньше, чем нужно, а затем «компенсируете» это в ответе. К примеру, при прибавлении 9 метод компенсации заключается в том, чтобы прибавить 10 и отнять 1:

Опять же, это работает и в случае вычитания.

267 – 48 проще представить себе как 267 – 50; это равно 217. Но ведь при этом мы отнимаем на 2 больше, чем нужно (нам надо вычесть не 50, а 48), так что ответ следует подправить, вернув 2 на место: получится 219.

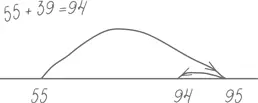
Научившись демонстрировать ход своих рассуждений при помощи неразмеченной числовой прямой, ребенок может приступить к изобретению других методов, работающих с конкретными типами чисел: 55 + 39 =

Здесь можно было бы добавить сначала 30, а затем 9, но, будучи уверенными в своих силах, мальчик или девочка могут попробовать и иной способ: сначала прибавить 40, а затем вычесть 1.

Ваш ребенок в школе будет учиться не только тому, как выполнять сложение или вычитание; он должен также усвоить, когда следует применять каждую из этих операций. Как правило, дети без труда понимают, в каком случае нужно что-то складывать, но вычитание в этом плане воспринимается хуже.

Многие люди читают примеры вроде 37 – 19 как «от тридцати семи отнять девятнадцать»: их первые впечатления о работе с вычитанием связаны с тем, что что-то убирают или отнимают. Отсчитываем 37 счетных палочек, а теперь 19 убираем, сколько остается? Но ведь при помощи вычитания можно решать множество самых разных задач, в том числе тех, где ничего не «отнимается».

У меня 37 наклеек, а у моего друга 19. На сколько наклеек у меня больше?

Эту задачу можно решить вычитанием: 37 – 19, но ничего здесь ни у кого не отнимается – в конце концов я останусь при своих 37 наклейках, а у моего приятеля их по-прежнему будет 19.

Аналогично, предположим, что новая игра для игровой приставки, о которой я мечтаю, стоит £37. Пока в моей копилке набралось £19. Сколько еще мне нужно накопить?

Дети склонны решать такие задачи при помощи счета вверх от 19 до 37, что можно записать как 19 +? = 37, но вы можете перевернуть пример и спросить: «Чему равно 37 – 19?»

В этом случае неразмеченная числовая прямая также представляет собой мощный образ и помогает ребенку освоить методы вычитания в уме, а также исследовать различные его смыслы. Мы предлагаем вам подумать чуть-чуть над следующими тремя примерами: прежде чем читать дальше, попробуйте найти ответы и осмыслить, как вы это сделали:

130 – 17; 130 – 118; 130 – 49.

Первый пример большинство людей решает путем «отъема»: они удаляют 17 из 130, как правило сначала отнимая 10 и получая 120, а затем отнимая 7 и получая 113. Но «отнимать» 118 из 130 – довольно громоздкая процедура. Проделать это можно, но вы, скорее всего, сказали себе: «Так, 12 и 118 будет 130». Иными словами, вы, вместо того чтобы «отнимать», добавляли к 118 и по существу искали разницу между двумя числами. 130 – 49 иногда подталкивает к другой «компенсационной» стратегии: 49 близко к 50, поэтому вычтем 50 из 130, получим 80 и добавим единицу обратно (в порядке компенсации за ту лишнюю единицу, которую мы вычли, когда вычитали 50 вместо 49). Все эти методы можно наглядно представить на неразмеченной числовой прямой.

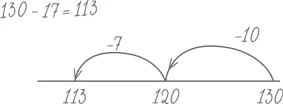
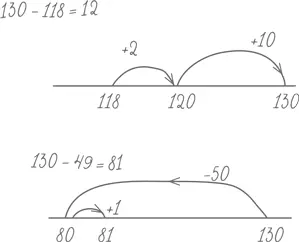
Многие учителя сегодня рекомендуют детям сопровождать счет такими вот короткими то ли рисунками, то ли записями, потому, что, по данным психологов, дети постепенно начинают работать с каким-то воображаемым вариантом числовой прямой и в дальнейшем могут складывать и вычитать уже без всяких записей.

Работая с детьми, старайтесь использовать самые разные слова при чтении задач на вычитание. Так, когда есть пример 10 – 7, вы можете сказать: «От десяти отнять семь», «Десять минус семь», «Из десяти вычесть семь», «Какова разность между десятью и семью», «На сколько десять больше семи?», «Насколько семь меньше десяти?»