Роб Истуэй - Математика для мам и пап - Домашка без мучений

Начав учиться в школе, ребенок и правда учится складывать и вычитать абстрактные числа: 3 + 5, 7 – 4 и т. д. При этом он заучивает так называемые факты сложения [3], как может объявить вам ваш ребенок или его учительница. Это начало путешествия детей в страну устного счета – математического навыка, которому в сегодняшней начальной школе уделяется гораздо больше внимания, чем в прежние времена.

Идеальное средство помочь ребенку как следует усвоить состав чисел – игра. Любая настольная игра с двумя кубиками заставляет мальчика или девочку тренироваться в сложении случайных чисел от 1 до 6. Вы без труда можете приспособить любую классическую игру-бродилку для игры с двумя кубиками. Сначала можно немного «подправить» один из кубиков, наклеив на грани стикеры и обозначив три из них одной точкой, а другие три – двумя. Бросание двух кубиков – такого вот упрощенного и стандартного – создает условия для того, чтобы ребенок попрактиковался в прибавлении к числу единицы и двойки – а это ключевое умение для маленького ребенка.

Домино тоже хорошо помогает усвоить состав чисел. Дайте сыну или дочери посмотреть на костяшку столько времени, чтобы он мог понять, сколько там точек с той и другой стороны, но не успел сосчитать все точки вместе. Сможет ли он определить суммарное количество точек? Переверните костяшку, пусть ребенок проверить результат.

Одним из удивительных результатов исследования того, как дети складывают и вычитают, стало следующее открытие: оказывается, развитию навыков устного счета помогает использование бумаги и карандаша! Речь идет об использовании их не для традиционных вычислений столбиком, а для облегчения решения не требующих сложных расчетов задач. Если отмечать на бумаге то, что происходит в голове, и фиксировать промежуточные шаги, то вашему ребенку будет проще рассказать, что он делает, – и в следующий раз вспомнить приемы устного счета.

Умение складывать – естественный результат развития навыка простого счета, и рано или поздно наступает ключевой момент, когда ребенок понимает: чтобы сложить пять конфет и четыре конфеты, не обязательно считать все девять: можно начать с пяти и посчитать после этого еще четыре. В школе для этого используют числовую прямую; от цифры 5 проводят стрелку, добавляя таким образом 4 и получая 9.

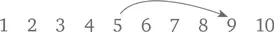
По мере того как добавляемые числа становятся больше, полезно бывает разбить процесс сложения на шаги. Вместо того чтобы складывать 8 и 7, дети могут сначала прыгнуть от 8 на 2 (чтобы получить 10), а затем прыгнуть еще раз, на оставшиеся 5, чтобы получить 15.

Разделение числа на части известно сегодня в начальной школе под громким названием – «разбиение». (Большинство родителей, конечно, знакомы с этой идеей, – просто раньше для нее не придумывали специального названия!) Как вы увидите в дальнейшем, знание о разбиении понадобится при изучении всех разделов арифметики, так что стоит добавить это слово в свой словарь.

Простейшие примеры на вычитание решаются точно так же, только двигаться по числовой прямой нужно справа налево, а не слева направо. Так что пример 12 – 5 можно реализовать либо одним прыжком налево, либо в два этапа, к примеру, как показано ниже.

Как только ребенок усвоил базовые факты сложения (для чисел от 1 до 10), он оказывается готов к овладению новыми навыками устного счета. Сегодня детям рекомендуют мысленно представлять себе неразмеченную числовую прямую, на которую при расчетах они будут помещать числа.

Благодаря числовой прямой дети начинают открывать для себя, что существует много различных методов, которые можно использовать при сложении.

Рассмотрим пример: 55 + 37

Если ваш ребенок уже уверенно складывает и вычитает в уме и имеет базовое представление о разрядных значениях, то он, вполне возможно, изобретет для себя метод решения подобных примеров, основанный на разбиении обоих чисел на десятки и единицы: