Роб Истуэй - Математика для мам и пап - Домашка без мучений

Теперь обведите кружком любое число из оставшихся – и опять вычеркните все числа в его строке и столбце. Проделайте ту же операцию в третий раз – и наконец обведите кружком единственное оставшееся число таблицы. Теперь у вас есть четыре числа, которые вы сами выбрали. Сложите их. Чему равна сумма? 19?

1. Нарисуйте таблицу, состоящую из четырех строк и четырех столбцов.

2. Напишите карандашом восемь чисел, которые в сумме дают волшебное число – в данном случае 19, вдоль верхней границы таблицы и сверху вниз по левому краю. Очень хорошо, если все числа будут разными, но это не обязательно. К примеру, вы можете выбрать следующие восемь чисел (проверьте, дают ли они в сумме 19):

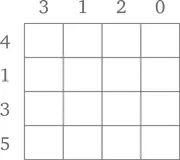
3. Теперь заполните клетки таблицы числами, полученными при сложении числа, написанного над столбцом, и числа, указанного слева от строки. К примеру, в левой верхней клетке таблицы должно стоять 3 + 4, поэтому впишите туда 7 (у вас получилась так называемая таблица сложения). Как будет выглядеть частично заполненная таблица, см. далее.

4. Сотрите числа, написанные карандашом вокруг таблицы. Волшебный квадрат готов к использованию.

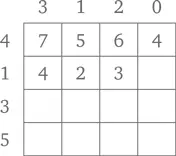
Теперь всякий раз, когда вы выберете ровно по одному числу из каждого столбца и каждой строки, сумма выбранных чисел составит 19.

Чтобы составить волшебный квадрат с иной суммой (к примеру, она будет равняться 43), просто позаботьтесь о том, чтобы числа вдоль границ таблицы на Шаге 2 из перечисленных выше в сумме давали 43. Из волшебных числовых таблиц получаются замечательные открытки ко дню рождения. Просто нарисуйте на открытке соответствующую таблицу – и позаботьтесь о том, чтобы в сумме числа составляли возраст того, кому эта открытка предназначается.

Метод вычитания при помощи числовых прямых работает в точности так же, как и в случае сложения, но двигаться по прямой при этом приходится влево, а не вправо. Однако некоторые подходы к вычитанию оказываются проще других.

Скажем, взгляните на такой пример: 55 – 37 =?

Разбиение обоих чисел на десятки и единицы и попытка вычислять в уме может запутать ребенка, если только он не умеет свободно обращаться с отрицательными числами. Если не проявить достаточной осторожности, можно получить примерно следующее:

1. Вычитаем 30 из 50, получаем 20.

2. Вычитаем 7 из 5 (получаем –2). Могу я это сделать? Может быть, нужно вычесть пять из семи? Получится два.

3. Что же делать дальше? Прибавить два к 20, вычесть два из 20, или что? Помогите!!!

Все будет намного проще, если вы начнете с целого первого числа (в данном случае 55) и вычтете из него сначала десятки, а потом единицы.

1. Вычитаем 30 из 55, получаем 25.

2. От 25 отнимаем семь. Ответ – 18.

Логику, лежащую в основе этого метода, опять же можно прекрасно проиллюстрировать при помощи неразмеченной числовой прямой.

Выполните этот пример на вычитание, а затем сравните свой ответ с ответом девятилетнего ребенка: 73 – 28 =

Приемы устного счета эффективны в том случае, когда дети в состоянии складывать в уме небольшие и крупные числа или вычитать небольшие числа из более крупных. Здесь полезны два метода, которые одинаково хорошо работают и со сложением, и с вычитанием.

Первый метод называется мостиком, или переходом, через десяток. Если вы хотите прибавить, скажем, шесть к 137, полезно подумать о разбиении шестерки: сначала добавляем три к 137, затем «отскакиваем» от 140 и добавляем оставшиеся три. Вот как ребенок показал, как это делается, на пустой числовой прямой:

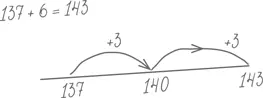
Аналогично для вычитания.