Роб Истуэй - Математика для мам и пап - Домашка без мучений

4. Дети думают, что нельзя вычесть большее число из меньшего, поэтому решить пример 7 – 11 невозможно (слава богу, в банке так не считают).

Давным-давно, по крайней мере так рассказывают, жил на свете восьмилетний мальчик по имени Карл Фридрих Гаусс. У него был плохой учитель, который хотел, чтобы дети работали, пока сам он сидит и занимается чем-то посторонним. Поэтому учитель задал детям длиннющий пример:

1 + 2 + 3 + 4 + 5 + … и так до 100.

«Это должно занять их почти до конца урока», – подумал учитель, уверенный, что детям придется много считать на бумаге. Но уже через минуту Гаусс поднял руку: «Сэр, я получил ответ». Мальчик нашел весьма хитроумное решение: мы расскажем о нем в конце главы. (Если вы хотите сами поразмыслить о том, как Гауссу удалось выполнить задание так быстро, вот намек: что, если написать в ряд числа от 1 до 100, а под ними те же числа, но в обратном порядке, от 100 до 1?)

Гаусс вырос и стал знаменитым математиком, и мы не утверждаем, что многие дети в столь раннем возрасте способны проявить такие же математические способности, как Гаусс. Однако мы хотели бы, чтобы ребенок всегда задавал себе вопрос: «А не существует ли быстрого и эффективного способа вычислить это?» – а не просто считал бы «традиционным» способом. Многие примеры на сложение и вычитание, даже с большими громоздкими числами, можно решить быстрее и часто точнее с использованием приемов устного счета.

Одного восьмилетнего мальчика спросили: «Если малыш родился в 1998 году, то сколько лет ему исполнилось в 2001 году?» Он без колебаний ответил: «Три».

Этому же мальчику чуть позже дали пример: 2001 – 1998. Внезапно здравый смысл отказал ребенку и включился автопилот. Вот его расчет:

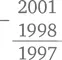
Он нашел разницу между цифрами в каждом столбце и записал ее. Проблема с вертикальными вычислениями состоит в том, что они заставляют сосредоточиться на цифрах в числе, а не на самих числах. Это означает, что ребенок, выполняя такие операции, проделывает все механически и не задумывается о разумности ответа.

Устный счет сегодня не похож и не должен быть похож на устный счет 1950-х и 1960-х гг. Тогда дети испытывали сильное давление – нужно было как можно быстрее отвечать на вопросы учителя, задаваемые всему классу, – и часто испытывали чувство стыда, если им не удавалось поспевать за всеми. (Один из нас, Майк, ходил в школу, где за промедление ученики получали удар линейкой по рукам. Логика такого отношения непонятна ему до сих пор.)

Устный счет нужен для того, чтобы человек мог посмотреть на предложенные числа и увидеть самый подходящий метод вычисления. Вам следует объяснить ребенку, что, прежде чем что-то считать на бумаге, нужно спросить себя: «А нельзя ли проделать это в уме?»

Рассмотрим такой пример: 2734 + 3562.

Числа здесь не выглядят особенно «дружелюбными», и самое разумное – взять лист бумаги и карандаш и посчитать столбиком.

Но как насчет этого: 3998 + 4997?

На первый взгляд очень похоже на первый пример. Однако секундное раздумье перед тем, как начать складывать в столбик, – и можно заметить, что оба числа приближаются к целому количеству тысяч, то есть к числам, кратным 1000: 3998 близко к 4000, а 4997 – к 5000. Сложить 4000 и 5000 несложно, это будет 9000. Теперь все, что нужно сделать, – это чуть-чуть подправить результат; он на 5 больше, чем нужно (2 от 3998 и 3 от 4997). Так что ответ 8995. Несмотря на то что описание кажется длинным и занимает несколько строк, все это проделывается очень быстро. Быстрее, чем взять бумагу и карандаш. И вероятность ошибки меньше.

Какой из этих примеров можно без труда решить в уме? Для каких потребуется бумага и ручка?

а. 152 +148

б. 300 – 148

в. 843 – 677

г. 843 – 698

д. 4997 + 5003

е. 6002 – 3999

Прежде чем разбираться в том, как помочь ребенку освоить методы устного счета, подобные упомянутому выше, полезно приглядеться к ранним стадиям обучения сложению и вычитанию.

Большинство из нас, взрослых, обучалось сложению и вычитанию так давно, что мы успели уже позабыть, как долго нам пришлось осваивать эти навыки. Обычный четырехлетний ребенок вполне способен сказать вам, что два банана плюс три банана будет пять бананов или два нагеля плюс три нагеля будет пять нагелей, даже если он представления не имеет, что такое нагель. Но спросите у него, сколько будет три плюс два, и ребенок посмотрит на вас с недоумением: для него это слишком абстрактно. (В классическом исследовании один четырехлетка на вопрос о том, сколько будет три плюс два, ответил: «Не знаю, я еще не хожу в школу».)