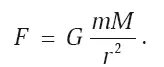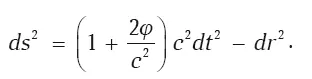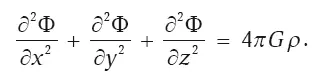Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Решить уравнения Эйнштейна – это значит найти коэффициенты g ab . Но гравитационные уравнения должны решаться вместе с уравнениями для материи, состояние и движение которой также должны стать известными, как результат найденного решения. Также часто решают гравитационные уравнения в вакууме, то есть для областей пространства-времени, где нет материи. Тогда задачей является определить только метрику g ab , анализ которой даст всю информацию об искривлении пространства-времени, его геодезических и т. д. Решение уравнений ОТО с бо́льшими деталями обсуждается в Дополнении 4.

После того как решение уравнений ОТО найдено, необходимо обратиться к принципам соответствия, которые были определены в конце предыдущего параграфа. Первый из них касается соответствия теории гравитации Ньютона. Принцип звучит четко и довольно жестко. Но так и должно быть, если мы не хотим ошибиться в интерпретации решений новой теории. Теория Ньютона в данном случае играет роль критерия.

Уже сейчас очень полезно для последующего изложения записать простые формулы этого соответствия. Мы уже говорили, что гравитация Ньютона представлена скалярным полем (потенциалом) φ. Для точечной массы M (или сферически распределенного вещества) скалярное поле вне вещества определяется как φ= – GM / r , где r – расстояние до центра тела. Тогда сила, действующая на тело массы m в этом потенциальном поле, определяется стандартной формулой закона всемирного тяготения:

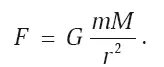
Движение тел в таком поле хорошо изучено. Как найти соответствие с движением тел в ОТО? Для этого нужно найти пространство-время, геодезические которого, в приближении малых скоростей и слабого поля φ, соответствуют движению тел в теории Ньютона. Такое пространство-время легко находится, его метрика в обсуждаемом приближении имеет в сферических координатах простую форму:

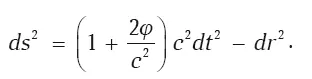
В силу сферической симметрии мы опустили угловую часть, оставив только временную и радиальную. Эту метрику иногда называют метрикой «пространства-времени Ньютона». Здесь g 00= 1 + 2j/ c 2= 1–2 GM / rc 2. Если нет тяготеющего центра, т. е. масса M = 0 , то поле φ исчезает и метрика обращается в метрику пространства Минковского.

Этим мы отметили соответствие для движения тел в теории Ньютона и ОТО. Но также необходимо показать, что для слабых гравитационных полей и малых скоростей уравнения релятивистской теории гравитации должны перейти в уравнения гравитации Ньютона. Но что такое уравнения тяготения Ньютона ? Очевидно, что это должны быть уравнения для поля φ. Здесь приходится идти обратным путем. Мы знаем, какое поле создается каждой отдельной частицей. Если у нас имеется произвольное распределение плотности вещества ρ в пространстве, то для каждой точки нужно выписать соответствующее значение φ. А общее поле Φ в каждой точке пространства просто сложится из всех отдельных φ. Тогда получится, что поле Φ в каждой точке удовлетворяет уравнению:

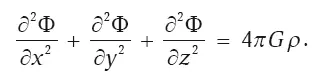
Оказывается, что при всех ограничениях соответствия уравнения ОТО, действительно, сводятся к этому единственному уравнению.

Но на проблему связи между теориями можно посмотреть и с другой позиции. Сила Ньютона – это обычная сила, которая растягивает пружину динамометра, давит на поверхность Земли, держит, как на «цепочках» (или «резинках»), планеты в Солнечной системе. В ОТО ситуация другая. Представим, что нас одарили «божественной» способностью воспринимать искривленное пространство-время. При этом мы в состоянии фантастически осознать, где там проходят геодезические (по аналогии с тем, что нашего реального восприятия достаточно, чтобы оценить, что шайба, брошенная по гладкой поверхности катка, движется равномерно и прямолинейно). Тогда для нас понятие гравитационной силы исчезло бы вообще. Все заменилось бы геометрией. Вместо воображаемых «цепочек», на которых Солнце «тащит» планеты, мы увидели бы нечто, похожее на воронку, в которой планеты свободно (по инерции) обращаются вокруг Солнца (рис. 6.3). Если какой-нибудь планете придать достаточно большую скорость, то она «выскочит» из воронки (а на языке гравитации Ньютона – преодолеет солнечное притяжение) и улетит в космос. Проявление же силы тяготения в быту мы интерпретировали бы как препятствие движению по геодезическим. Так, и пружина динамометра, и поверхность Земли, препятствуют такому движению.