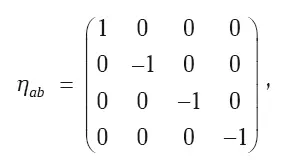Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Логика построения уравнений Эйнштейна и их конкретный формальный вид даны в Дополнении 3, а здесь мы разъясним основные понятия ОТО, к которым будем часто обращаться в основном тексте. Вернемся к понятию интервала, который был введен для пространства Минковского. В отличие от плоского пространства, в искривленном пространстве-времени расстояние между двумя мировыми точками в общем случае невозможно определить как конечную длину отрезка прямой. Необходимо перейти к измерениям в малой окрестности мировой точки (к бесконечно малым величинам). Тогда квадрат интервала пространства Минковского между двумя бесконечно близкими точками перепишется как квадрат элемента интервала (уже бесконечно малой величины) в виде:

ds 2= c 2 dt 2– dx 2– dy 2– dz 2.

Элемент пространства Минковского имеет такой простой вид еще и потому, что здесь используются координаты Лоренца, то есть декартовы координаты в совокупности с временной координатой. Этот же квадрат элемента интервала (часто его все равно называют «интервал») может быть записан в более формальном виде:

ds 2= η abdx adx b .

Здесь a, b = 0, 1, 2, 3; а нулевой координате обычно приписывают смысл временной, умноженной на скорость света: x 0= ct . Величина η ab является диагональной (отличны от нуля только элементы на диагонали) матрицей 4 × 4,

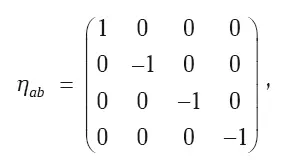
и называется метрикой Минковского. Формальная запись интервала перейдет в уже привычную, если использовать простое правило суммирования по повторяющимся индексам, например: m a n a = m 0 n 0+ m 1 n 1+ m 2 n 2+ m 3 n 3. Метрика η ab задает способ измерения расстояний в пространстве Минковского в лоренцевых координатах.

Давайте «искривим» координаты (сделаем их произвольное преобразование), тогда интервал примет вид:

ds 2= g ab dx adx b .

Величина g ab также называется метрикой и фактически задает способ измерения расстояний в пространстве Минковского, но в тех координатах, в которых она определена.

Важно отметить, что элемент ds , так же как и сам интервал, инвариантная величина, то есть его значение остается тем же в любых координатах. Метрика g ab – это тоже матрица 4 × 4, но теперь в общем случае она уже не диагональна, ее компоненты g 00 , g 01 , g 11 , g 12 … могут быть какими-либо функциями времени и пространственных координат, см. Дополнение 1.

В искривленном пространстве-времени способ измерения расстояний между мировыми точками такой же, как в плоском в криволинейных координатах – с помощью элемента интервала. Разница в том, что для пространства Минковского возможен переход от g ab к простому диагональному виду η ab во всем пространстве-времени, а для искривленного – нет. Однако в малой окрестности отдельного свободно падающего наблюдателя такой переход возможен. Ведь согласно слабому принципу эквивалентности он ощущает себя в инерциальной системе отсчета! Искривление не позволяет связывать мировые точки прямыми, поэтому мировые линии (геодезические или нет), соединяющие события, будут в общем случае кривыми. Их длина вычисляется с помощью бесконечно малых элементов интервала и последующего интегрирования.

Как элемент интервала, так и длина мировых линий (их полный интервал), также являются инвариантными по отношению к преобразованиям координат.

Пространственно-временные измерения и фиксация метрических свойств осуществляются также с помощью света. Скорость света не зависит от скорости излучателей, а для каждого локального наблюдателя, измеренная в его собственной системе отсчета, имеет одно и то же стандартное значение c . При измерениях самым важным является то, что для света элемент интервала ds в силу инвариантности всегда равен нулю.

Если в наше время спросить даже не самого сведущего, но все-таки образованного, человека: уравнения Эйнштейна – это уравнения чего? С большой вероятностью получишь ответ, что это уравнения гравитационного поля. А что такое гравитационное поле мы фактически только что рассказали – это поле метрики g ab , или метрического тензора.

Именно это поле дает возможность построить величины, определяющие искривление пространства-времени. Тензорное поле определяется аналогично тому, как определяются скалярное и векторное поля. Задать поле метрического тензора означает, что в каждой мировой точке пространства-времени нужно задать набор функций, каждая из которых соответствует одной из компонент матрицы, представляющей этот тензор.