Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Точно так же, как была представлена пространственно-временная диаграмма для сопутствующих наблюдателей в координатах Леметра, можно представить пространственно-временную диаграмму для равномерно ускоренных наблюдателей. Для этого каждому такому наблюдателю сопоставляют свою пространственную координату со значением X. Тогда метрика пространства Минковского (вернее его части, заключенной в углу Ринд-лера), в координатах этих ускоренных наблюдателей принимает форму:

ds 2= ( X / X 0) 2 c 2 dT 2– dX 2– dY 2– dZ 2.

Здесь X 0– произвольный пространственный масштаб, позволяющий сохранить размерность, кроме того, для наблюдателя, у которого X = X 0, эта система является локально лоренцевой. Эти координаты введены американским физиком Вольфгангом Риндлером, и представлены на диаграмме на рис. Д3. Каждому ускоренному наблюдателю соответствует вертикальная прямая с соответствующим значением X. Вертикальная прямая X = 0 соответствует горизонту Риндлера. Если время T является координатным временем в системе Риндлера, то собственным временем для ускоренного наблюдателя является τ = ( g 00) 1/2 T = XT / X 0, как это было определено в главе 7.

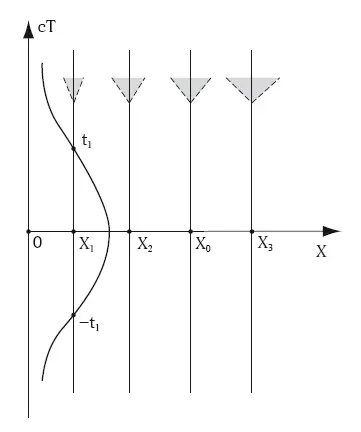
Рис. ДЗ. Координаты Риндлера

Для ускоренного наблюдателя с параметром X 0собственное время совпадает с координатным. Собственное время ускоренных наблюдателей идет тем быстрее, чем больше X , и тем медленнее, чем меньше X . В этом проявляется сильный принцип эквивалентности (глава 6) – ускорение имитирует действие гравитационного поля, где ход часов замедляется тем сильнее, чем больше потенциал.

На горизонте собственное время «замораживается», в этом смысле ситуация аналогична поведению собственного времени для наблюдателей в пространстве-времени шварцшильдовой черной дыры. Если мы проследим за формой светового конуса, то для наблюдателя X 0его «лепестки» наклонены под «стандартным» углом 45° (это как раз потому, что для него система Риндлера оказалась локально лоренцевой). Для больших X угол наклона «лепестков» увеличивается, для меньших X – уменьшается. На горизонте «лепестки» световых конусов вообще слипаются, точно также, как на горизонте на диаграмме Шварцшильда, см. рис. 8.2. Горизонт в метрике Риндлера представляет лишь координатную особенность, как и горизонт в координатах Шварцшильда. Но поскольку система ускоренных наблюдателей – это система в пространстве Минковского, то в отличие от решения Шварцшильда, «решение Риндлера» не имеет истинной сингулярности.

Наконец, обратимся к мировой линии покоящегося наблюдателя в пространстве Минковского – на рис. Д2 вертикальная линия x 1= const. Она соответствует кривой линии на рис. Д3. Координаты Риндлера охватывают лишь часть пространства Минковского, как видно из рис. Д2, поэтому ясно, что кривая на рис. Д3 отвечает лишь части истории покоящегося наблюдателя на рис. Д2.

Приведем более строгие, чем в главе 6, определения однородности и изотропии. Почему это важно? Эти понятия определяются на данный момент времени, а космологическое пространство меняется со временем. В теории Ньютона в этом нет проблемы, поскольку понятие времени абсолютно. В СТО тоже нет больших проблем, определившись с выбором какой-либо инерциальной системы отсчета, наблюдатель также имеет единое время. А в ОТО, да еще в переменном по времени решении, ситуация сложнее. Поясним это на примере того же решения Фридмана: ds 2= c 2 dt 2– a 2( t ) dl 2. Здесь каждому значению времени соответствует пространство со своим значением масштабного фактора a ( t ). Пространство-время как бы распадается на слои – пространства, сложенные «стопочкой». Ход времени определяется переходом от одного слоя (пространственного сечения) к другому, а каждый слой отвечает своему единственному моменту времени.

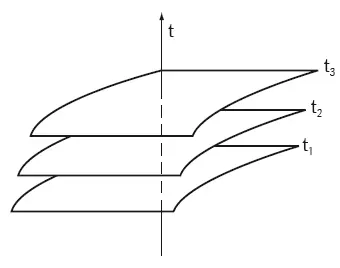
Рис. Д4. Расслоение пространства-времени на пространственные сечения

На рис. Д4 такое расслоение произвольного пространства-времени изображено символически, каждый слой – это 3-мерное пространство в данный момент времени. Для вселенной Фридмана каждое такое 3-мерное пространство и однородно, и изотропно. Но это произошло потому, что для поиска решений Фридман специально выбрал такую удобную систему координат именно с этим определением времени. На самом деле можно выбрать другую систему координат, для которой сечения одновременности уже не будут ни однородными, ни изотропными. В неоднородной же Вселенной подобрать однородные пространственные сечения вообще невозможно.