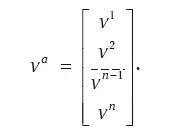Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

В основном тексте и далее в Дополнениях мы используем понятия скалярного, векторного и тензорного полей. Чтобы не было дискомфорта при встрече с этими терминами, дадим некоторые пояснения. Лучше начать с вектора. В обычном 3-мерном пространстве он определяется тремя компонентами – проекциями на оси x, y, z . Если представить себе n -мерное пространство, то для определения в нем вектора нужно задать набор n компонент. Тогда говорят, что задано поле вектора и его обозначают, например, v a , где a пробегает все координаты, от 1 до n , в общем случае, если мы их пронумеровали. А все n значений v a и есть те самые n компонент, часто их записывают в виде строки v a = [ v 1, v 2, …, v n–1, v n] или столбца

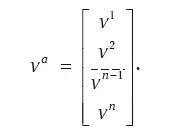
Величина v a (набор значений) с одним индексом называется тензором 1-го ранга. Поле скаляра, в отличие от вектора, в каждой точке пространства, независимо от его размерности, имеет одну компоненту (функцию от пространственных координат) и записывается как величина без индексов, скажем, v. Скаляр, как величина без значков, является тензором нулевого ранга. В тексте очень часто встречается понятие метрического тензора g ab , который и описывает гравитационное поле. Теперь, имея представление о векторе и скаляре, как о тензорах, смело можно говорить, что метрика – это тензор 2-го ранга и все его компоненты объединены в матрицу. В 4-мерном пространстве-времени это выглядит так:

В силу симметрии g ab = g ba независимых компонент из 16-ти остается 10. Поле метрического тензора задано, если в каждой точке пространства-времени задано 10 функций, представляющих эту матрицу. Аналогичные рассуждения справедливы для других тензоров второго ранга. Если бы мы хотели рассмотреть какой-нибудь тензор 3-го ранга, мы должны были представить величину с 3-мя индексами, а ей сопоставить 3-мерную матрицу (куб). Важно отметить, что все тензоры обладают общим свойством: при преобразованиях координат они преобразуются по специальному тензорному закону, сохраняя свою прежнюю структуру. Нетензорные величины при преобразованиях координат обычно приобретают дополнительные (по отношение к тензорным) слагаемые.

В тексте обсуждается и утверждается, что искривление пространства-времени – это результат воздействия материальных источников. Что они собой представляют и как представлены формально? Эти источники являются материей в самом общем понимании. Они включают в себя все вещество, которое может быть сосредоточено в отдельных телах или распределено дисперсно, и все возможные поля, как статические, так и поля излучения. Обсуждая специальную теорию относительности, мы уже отметили, что энергию и импульс в релятивистской теории нельзя рассматривать отдельно, а правильно рассматривать 4-мерный вектор энергии-импульса, скажем, материальной частицы. Но оказывается, что в искривление пространства-времени свой вклад вносят и другие характеристики материи, такие как напряжения внутри тел, давление Все вместе они образуют тензор энергии-импульса материи T ab .

Далее нам необходимо вспомнить об уравнении непрерывности. Суть его в том, что изменения со временем плотности вещества в данной точке равно скорости притока и оттока со всех сторон. Это один из законов сохранения, иначе его называют уравнением баланса, и он является следствием уравнений движения для вещества. Обобщение этого закона для всего тензора энергии-импульса в искривленном пространстве-времени означает, что он также должен удовлетворять закону сохранения.

Теперь мы в состоянии построить уравнения гравитации в ОТО. Как мы рассказали в главе 6, в начале XX века было постулировано, что гравитационное взаимодействие выражается в искривлении пространства-времени. При этом пространство-время искривляется под воздействием материи, которая, в свою очередь, движется в этом искривленном собой пространстве-времени. Это и есть логическая основа для построения уравнений общей теории относительности. Но как их построить правильно?