Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

В реальности не все пары дней рождения будут независимы друг от друга. Если у человека A дата рождения совпадает с датой рождения человека B, а у того – с датой рождения человека C, то даты рождения в паре A – C тоже совпадают, и, следовательно, не являются независимыми. Если бы они были независимыми, то шанс иметь общую дату рождения у них составлял бы только 1/365. Точный расчет вероятности совпадения с учетом этих зависимостей лишь немногим сложнее, чем при независимых величинах в предыдущем абзаце. При таком расчете мы добавляем людей «в комнату» по одному. Как мы уже установили, для двух человек вероятность несовпадения даты рождения составляет 364/365. Когда к ним добавляется третий, дата рождения каждого из трех может приходиться на любой из оставшихся 363 дней в году (если у кого-то не обнаружится общая дата рождения с кем-то из оставшейся пары). Таким образом, вероятность того, что у трех человек не совпадут даты рождения, составляет (364/365) × (363/365). Четвертому достается уже только 362 дня, поэтому вероятность, что даты рождения не совпадут у четверых, несколько снижается – до (364/365) × (363/365) × (362/365). Этот ряд продолжается до тех пор, пока к вечеринке не присоединится последний, 23-й участник. Его день рождения может выпасть на любой из оставшихся 343 дней. Вероятность того, что ни у кого из 23 человек даты рождения не совпадут, определяется последовательным перемножением:

364/365 × 363/365 × 362/365 ×… ×343/365

Это выражение свидетельствует: точная вероятность, что даты рождения всех 23 человек отличаются (с учетом возможных зависимостей), составляет 0,4927, что чуть меньше 1/2. Используя принцип исчерпывающего множества комбинации величин (утверждающий, что единственными вариантами в нашем случае является либо отсутствие совпадений, либо наличие как минимум одной общей даты рождения), получаем, что вероятность совпадения дат составляет 0,5073, что немного больше 1/2. Если в группе будет 70 человек, количество возможных пар вырастет до 2415. Точный расчет в таком случае дает почти абсолютную вероятность совпадения – 0,999. На рис. 16 показано, как изменяется вероятность того, что два события произойдут в один день, по мере роста числа рассматриваемых независимых событий с одного до ста.

Для несведущего в математике человека такая высокая вероятность может оказаться неожиданной. Я воспользовался этим приемом, чтобы произвести впечатление на моего литературного агента, когда мы в первый раз обсуждали перспективы данной книги. Я поспорил с ним на выпивку, что найду в относительно немноголюдном пабе хотя бы пару человек, даты рождения которых совпадают. Окинув взглядом помещение, он с готовностью принял пари – и даже поднял ставки, предложив оплатить два раунда выпивки, если я смогу найти такую пару; он совсем не верил в такую возможность. Спустя двадцать минут, множества озадаченных взглядов и несколько легких оправданий («Все в порядке, – поясняла моя слегка потрепанная ипостась людям, к которым я приставал с расспросами, – я математик!»), я нашел свою пару именинников, так что выпивка была за счет Криса. Наверное, это было не совсем честно с моей стороны – покупая выпивку первый раз, я уже подсчитал количество посетителей в баре. Их было около 40, и я знал, что с таким числом участников я мог проиграть пари с мизерной вероятностью в 11 %. Я должен был ставить два к одному против Криса, а не наоборот. Разумеется, высокая вероятность совпадений при удивительно малом количестве событий имеет несколько более глубокие последствия, чем небольшой математический розыгрыш простодушной жертвы в баре. В частности, это может помочь нам проверить вывод Горки о том, что исламисты способны наносить удары в любой момент, когда захотят.

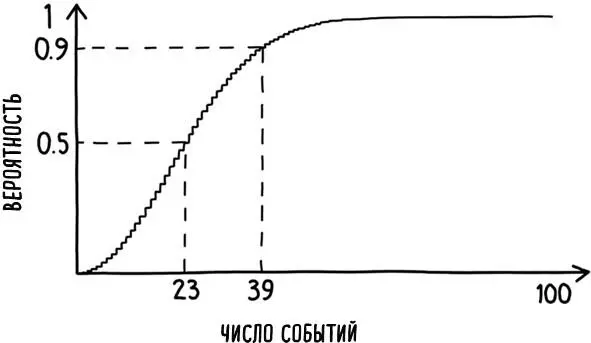
Рис. 16. Вероятность наступления двух и более событий в один и тот же день возрастает с увеличением количества событий. При наличии 23 событий вероятность совпадения чуть выше 1/2. При наличии 39 независимых событий вероятность того, что в один день произойдут как минимум два из них, возрастает почти до 0,9

За пять лет с апреля 2013 по апрель 2018 года исламистские террористы совершили не менее 39 терактов против западных государств (Европейского союза, Северной Америки или Австралии). На первый взгляд кажется маловероятным, что два из них выпали на одну и ту же дату, если бы их разброс по году был действительно случаен. Однако, поскольку из 39 событий можно составить 741 пару, вероятность, что два из них придутся на одну и ту же дату, очень высока – около 88 %, как показано на рис. 16. С такой высокой вероятностью удивительно было бы, если бы даты двух каких-нибудь терактов не совпали. Конечно, это ничего не говорит о вероятности будущих терактов, но, похоже, Горка серьезно переоценил организационные навыки исламистов.