Нанеся на карту положения тех или иных деталей по нескольким последовательным снимкам, измеряем затем по карте их смещения между двумя соседними положениями. Поделив эти смещения на интервалы времени между снимками, получим значения скоростей движения этих деталей.
Впрочем, производить измерения по карте не обязательно — необходимые нам смещения можно вычислить. Пункт наблюдения и оба положения проекции детали серебристого облака образуют сферический треугольник на поверхности земного шара (рис. 44), в котором мы без труда находим две стороны s 1, s 2(угол между^ними α = А 1— А 2нам известен), зная расстояния S 1, S 2:
s 1,2= (180/π)∙( S 1,2/ R). (34)
Здесь R = 6389 км — радиус кривизны земной поверхности в широтном поясе, где наблюдаются серебристые облака. Третью сторону треугольника λ найдем по формулам
где β — вспомогательный угол, противолежащий стороне s 2.
Рис. 44. Сферический треугольник на поверхности Земли (к определению смещения серебристых облаков).
От величины λ — дуги смещения в градусах — делаем переход к смещению L в километрах по формуле
L= (π∙ λ/180)∙ R. (37)
Поделив L на интервал времени t , получим скорость движения данной детали серебристого облака. Скорости надо свести в таблицу для данной ночи, и если они мало отличаются друг от друга, найти среднюю скорость. Потом надо сопоставить между собой скорости движения для разных ночей, построить график распределения по скоростям.
§ 15. Определение высот серебристых облаков
Определить высоты серебристых облаков можно из одновременных (корреспондирующих) фотографий, полученных с двух концов базиса, длина и ориентировка которого известны. Существует несколько способов определения высот серебристых облаков. Мы здесь изложим сравнительно простой способ, предложенный М. А. Дирикисом и Ю. Л. Францманом.
Введем прямоугольную геоцентрическую систему координат с началом в центре Земли. Ось X направим к точке пересечения экватора с начальным (гринвичским) меридианом, ось Y — к точке экватора с восточной долготой 90°, ось Z — к северному полюсу Земли.
Далее введем две топоцентрическне системы координат с началом в каждом из двух пунктов наблюдений. Оси расположим параллельно осям основной геоцентрической системы.
Определенные путем измерения на фотографиях горизонтальные координаты точки облака h, А переводим в экваториальные координаты t, δ по известным формулам
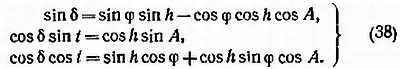
В формулах (38) φ — широта пункта наблюдения, δ — склонение, t — часовой угол данной точки облака. Далее для сокращения записи там, где формулы одинаковы для обоих пунктов, мы будем писать индекс i ( i = 1, 2). Топоцентрические координаты точки С облака будут равны
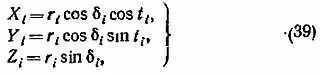
где r i— расстояния до точки С от обоих наблюдательных пунктов по прямой (по лучу зрения). Введем обозначения (для краткости)
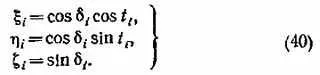
Тогда получим следующую систему из шести уравнений пятью неизвестными — геоцентрическими координатами точки С ( Х с, Y c, Z c) и расстояниями r 1, r 2:
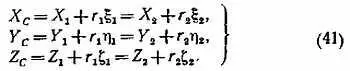
Эту систему можно решить методом наименьших квадратов, изложенным в Постоянной части «Астрономического календаря» (7-е изд. — М.: Наука, 1981, с. 521–532). Для тех, кто не знаком с этим методом, можно рекомендовать следующий порядок вычислений.
Отвлечемся на время от левых равенств в системе (41) и от величин Х с, Y c, Z c. Тогда у нас останутся три условных уравнения с двумя неизвестными r 1, r 2. Их решение по методу наименьших квадратов дает
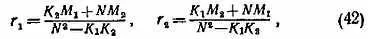
где введены обозначения
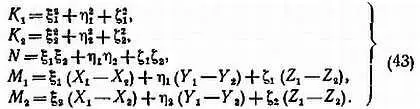
Подставляя r 1, r 2в уравнения (41), получим значения Х с, Y c, Z c. Из двух значений каждой из этих величин (по i = 1 и i = 2) берем среднее. Затем находим радиус-вектор точки С относительно центра Земли р с,
Читать дальше

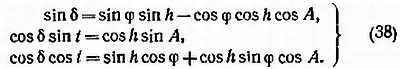
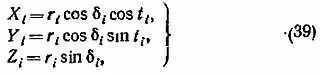
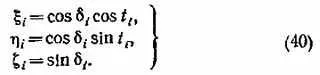
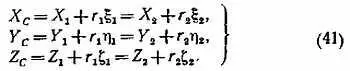
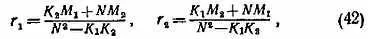
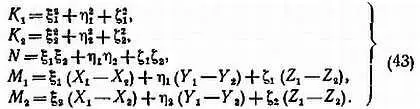


![Роберт Сальваторе - В тени лесов [Серебристые тени]](/books/337641/robert-salvatore-v-teni-lesov-serebristye-teni-thumb.webp)





