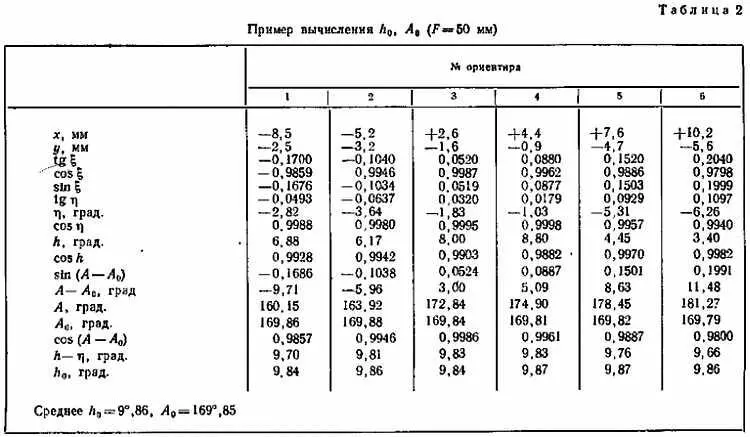
Хотя согласно правилам, изложенным выше, данные по ориентиру № 6 следует исключить из обработки, так как ( А — А 0) > 10°, этот ориентир дает значение h 0в хорошем согласии с остальными и лишь А 0для него «отскакивает» на 0°,06, т. е. на 3',6 от среднего значения.
Сейчас в продаже имеются микрокалькуляторы «Электроника», доступные по цене и позволяющие быстро вычислять логарифмы, тригонометрические и обратные тригонометрические функции. При использовании микрокалькуляторов надо иметь в виду, что и в работе с ними может быть допущена ошибка (как вычислителем — например, нажал не на ту кнопку, так и самим прибором), поэтому рекомендуется каждый расчет проводить дважды; лучше всего, если это делают разные вычислители (это называется вычислением «в две руки»). При наличии расхождений производится третий расчет. Если расчеты производятся с помощью таблиц и арифмометра (когда нет калькулятора), это тем более необходимо.
Итак, все необходимые величины нам известны, и можно приступить к операции развертывания фотографии.
Для измерения координат серебристых облаков на снимках удобнее всего приготовить специальную палетку. Если фотографирование ведется с малоформатной камерой типа «Зенит», измерять самый кадр неудобно, и нужно воспользоваться фотоувеличителем. Заложив кадр в фотоувеличитель, кладем на столик лист бумаги и подбираем масштаб увеличения, который в дальнейшем будем использовать при обработке всех снимков. Под этот масштаб мы и рассчитаем палетку.
Эффективное фокусное расстояние F ', соответствующее масштабу увеличенного изображения, равно
F' = F∙( L/ l), (30)
где F — фокусное расстояние объектива камеры, L и l — длины одних и тех же отрезков на увеличенном и оригинальном изображениях (это может быть любая из сторон кадра или его диагональ).
Формулы для расчета прямоугольных координат узловых точек палетки имеют вид
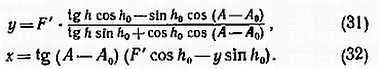
Задавая значения h, А через градус и зная F ', h 0, A 0,мы без труда найдем х, у для значений h, А — А 0, соответствующих целым градусам. Нанеся по значениям х, у точки на лист бумаги, соединим их отрезками прямых (из-за малой кривизны дуг нет надобности пользоваться лекалом). Пример такой палетки для F ' = 250 мм и h 0= 6°07′ представлен на рис. 41.
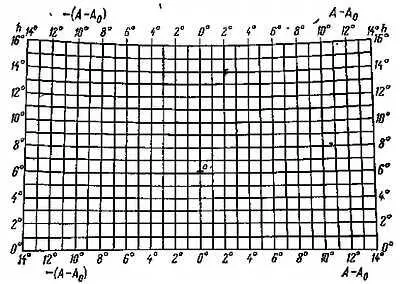
Рис. 41. Палетка для измерения координат серебристых облаков для F'= 250 мм и h 0= 6°07′
Теперь мы можем начать измерения. Накладываем палетку на изображение поля серебристых облаков так, чтобы линия горизонта и оптический центр, наколотый иголкой, на изображении совпали с соответствующей линией и точкой на палетке (рис. 42).
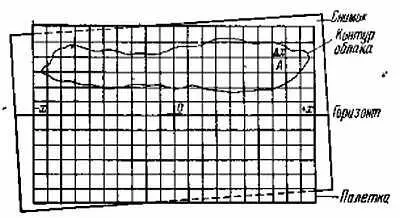
Рис. 42. Наложение палетки на снимок серебристых облаков.
Затем измеряем координаты h, А — A 0(которые потом переводим в h, А ) тех точек поля серебристых облаков, которые мы хотим отобразить на земную поверхность.
Расстояние S от точки наблюдения до проекции точки серебристого облака с учетом рефракции можно вычислить по следующей формуле, выведенной М. И. Буровым:
S= 7429∙(-tg h+ √(tg 2 h+ 0,0221)), (33)
где S — расстояние в километрах. Еще проще определить это расстояние с помощью номограммы, изображенной на рис. 43.
Рис. 43. Номограмма для определения расстояний.
Значения S приведены также в Приложении 3 в конце книги.
Определив S , берем хорошую географическую карту, помечаем на ней пункт наблюдений и откладываем от него расстояние S каждой точки поля серебристых облаков в направлении, соответствующем ее азимуту А (при этом надо помнить, что азимут 180° соответствует направлению на север). Мы получим проекции этих точек на земную поверхность. По отдельным точкам можно восстановить очертания всего облачного поля. Для удобства следует изготовить отпечаток снимка, зеркальный относительно линии горизонта: на этом отпечатке верх и низ поменяются местами, а левая и правая стороны останутся соответственно слева и справа. Такой отпечаток будет передавать общую конфигурацию облачного поля, но с перспективными искажениями. Напомним, что верхние части поля расположены ближе к нам, чем нижние, поэтому мы и рекомендуем изготовить такой зеркальный отпечаток. Кроме того, на нем будет наглядно видна волновая структура облаков (см. рис. 12).
Читать дальше


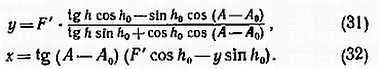




![Роберт Сальваторе - В тени лесов [Серебристые тени]](/books/337641/robert-salvatore-v-teni-lesov-serebristye-teni-thumb.webp)





