Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

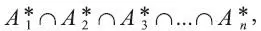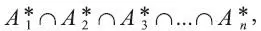
где Аi* – это либо А i , либо Аic . Заметим также, что:

1) имеется точно 2n таких фундаментальных произведений;

2) любые два таких фундаментальных произведения не пересекаются;

3) универсальное множество является объединением всех таких фундаментальных произведений.

Рассмотрим пример из трех множеств А, В и С и дадим геометрическую интерпретацию их фундаментальных произведений (рис. 1.7):

А = {1, 2, 3, 6, 7},

B = {3, 4, 5, 6},

C = {5, 6, 7, 8}.

Имеется ровно восемь фундаментальных произведений из трех множеств:

P 0 = A c ∩ B c ∩ C c = {9}

P 1 = A c ∩ B c ∩ C = {8}

P 2 = A c ∩ B ∩ C c = {4}

P 3 = A c ∩ B ∩ C = {5}

P 4 = A ∩ B c ∩ C c = {1, 2}

P 5 = A ∩ B c ∩ C = {7}

P 6 = A ∩ B ∩ C c = {3}

P 7 = A ∩ B ∩ C = {6}

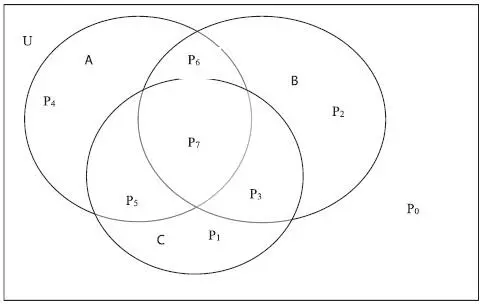
Рис. 1.7

Для данного множества S можно рассматривать множество всех его подмножеств. При этом придется рассматривать множество, элементами которого будут также множества, т. е. множество множеств. Чтобы избегать путаницы, часто бывает более удобно говорить о классе множеств или о семействе множеств. Если необходимо рассмотреть множества из данного класса, то можно говорить о подклассе или подсемействе. Например, рассмотрим множество S = { a, b, c, d }. Пусть А класс подмножеств S из трех элементов. Тогда

А = [{ a, b, c }, { a, b, d }, { a, c, d }, { d, c, d }].

Элементами класса А являются множества { a, b, c }, { a, b, d }, { a, c, d } и { b, c, d }].

Пусть теперь В класс подмножеств S , который содержит элемент а и два других элемента из S . Тогда

В = {{ a, b, c }, { a, b, d }, { a, c, d }]. Элементами В являются множества { a, b, c }, { a, b, d } и { a, c, d }]. Поэтому В является подклассом класса А.

Для данного множества S можно говорить о классе всех подмножеств S . Этот класс называют степенным множеством S и обозначают 2S. Если n ( S ) – число элементов множества S , то число элементов степенного множества n(2S) представляет собой степень 2 и равно n (2S) = 2 n(S). Например, если S = { a, b, c }, то степенное множество

2S = [ Ø ,{ a }, { b }, { c }, { a, b },{ a, c }, { b, c }, S ].

Заметим, что пустое множество Ø принадлежит к 2S, так как пустое множество является подмножеством S и само S принадлежит 2S, поэтому число элементов n(2S) = 23 = 8.

Рассмотрим теперь еще одно важное понятие, которое называется разбиением множества S . Разбиениеммножества S называется семейство { А i} непустых подмножеств S , для которых:

1) каждый элемент х из S принадлежит к одному из подмножеств А i;

2) подмножества из { А i} взаимно не пересекаются, т. е. если

А i ≠ А j, тогда А i ∩ А j = Ø .

Подмножества в разбиении иногда называют клетками или блоками. На рис. 1.8 представлена диаграмма Венна, изображающая разбиение прямоугольного множества точек S на пять клеток А 1, А 2, А 3, А 4, А 5.

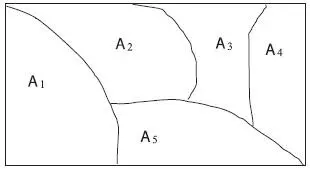
Рис. 1.8

Фундаментальные произведения также представляют собой разбиение универсального множества.

Операции объединения и пересечения могут быть распространены на любое количество множеств. Объединение состоит из таких элементов, которые принадлежат по крайней мере к одному из множеств, а пересечение из таких элементов, которые принадлежат ко всем множествам.

Абстрактная алгебра занимается изучением операций, производимых над некоторыми элементами. К настоящему времени идеи абстрактной алгебры используются не только для математических методов, но и позволяют получать практические результаты. Операции объединения, пересечения и дополнения, производимые над множествами, удовлетворят определенным законам (или тождествам) и образуют алгебру множеств. Поскольку числовая алгебра появилась раньше, то возникает вопрос, какая из операций (пересечение или объединение) «похожа» на операцию сложения чисел и какая – на операцию умножения. Ответить на этот вопрос едва ли возможно. Для чисел, например, выполняется только дистрибутивность умножения относительно сложения, а в алгебре множеств рассматривают два закона дистрибутивности: пересечения относительно объединения и объединения относительно пересечения.