Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

Важным при выполнении операций является их приоритет. Сначала выполняется операция дополнения, затем пересечения и затем объединения.

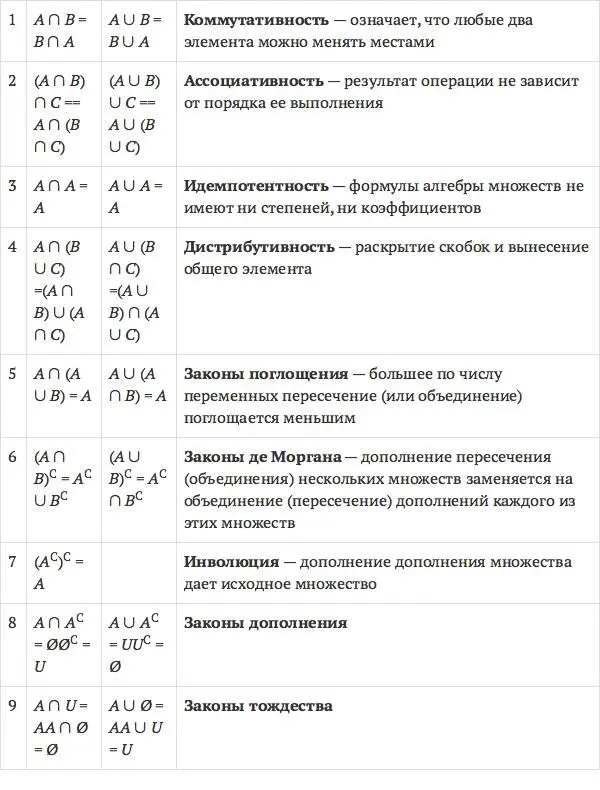
Множества удовлетворяют следующим законам (или тождествам):

Принцип двойственности алгебры множеств

Нетрудно заметить, что тождества в таблице располагаются парами, например первое тождество A ∩ B = B ∩ A имеет парное A ∪ B = B ∪ A, и это выполняется для всех остальных законов алгебры множеств.

Принцип двойственностисостоит в том, что если верно какое-либо тождество, то тождество, полученное из него путем замены каждой из операций ∩, ∪, а также U и Ø на операции ∪, ∩, Ø и U , соответственно, будет также верно. Поэтому у любого тождества есть его «двойник», отличающийся тем, что у него каждая операция замена на парную ей (объединение на пересечение, а пересечение на объединение) и при этом пустое множество заменяется на универсальное, а универсальное на пустое. Принцип двойственности очень важен, поскольку если доказана истинность какого-либо выражения, то истинность двойственного ему можно не доказывать – оно будет истинно вследствие данного принципа. Например, для верного тождества

A = ( A ∩ B C ∩ C C) ∪ ( A ∩ ( B ∪ C ))

двойственное ему будет также верным тождеством

A = ( A ∪ B C ∪ C C) ∩ ( A ∪ ( B ∩ C )).

Или для верного тождества

A = ( A ∩ U ) ∪ ( A ∩ B ∩ C ),

двойственное ему тождество A = ( A ∪ Ø ) ∩ ( A ∪ B ∪ C ).

Для доказательства равенства тождеств обычно используются четыре метода:

1) элементный метод;

2) диаграммы Венна;

3) табличный метод;

4) алгебраический метод.

Элементный методоснован на том, что для произвольно выбранного элемента x из множества, заданного в левой части тождества, доказывается, что этот элемент принадлежит и множеству правой части этого тождества. Затем выбирается произвольный элемент из правой части и показывается, что он входит и в левую часть. Вместе это доказывает, что оба множества состоят из одних и тех же элементов.

Докажем далее законы алгебры множеств.

Доказательство коммутативности(или сочетательного свойства) операций объединения и пересечения самоочевидно, поскольку ни в определении пересечения, ни в определении объединения ничего не говорится о порядке подмножеств.

Ассоциативность(или сочетательный закон) также просто доказывается. Покажем, что ( A ∩ B ) ∩ C ⊆ A ∩ ( B ∩ C ). Если x ∈ ( A ∩ B ) ∩ C , то x ∈ ( A ∩ B ) и x ∈ С , из x ∈ ( A ∩ B ) следует, что x ∈ А и x ∈ B , т. е. x принадлежит всем трем множествам A, B и C . Следовательно, x ∈ ( B ∩ C ) и x ∈ A ∩ ( B ∩ C ). Обратное включение показывается аналогично, поскольку множество в правой части тождества также образовано из элементов (и только из таких), которые входят в каждое из множеств A, B и C . Ассоциативность для операции объединения следует из того, что элементы в множестве левой части тождества и элементы в множестве правой части состоят из таких и только таких элементов, которые принадлежат по крайней мере одному из подмножеств A, B и C .

Идемпотентностьозначает, что если x ∈ A ∩ A , то, значит, x принадлежит пересечению множества A с самим собой, т. е. x принадлежит самому множеству A . Если элемент x ∈ A ∪ A , то x принадлежит объединению множества A с самим собой, т. е. и в этом случае он принадлежит только множеству A .

Докажем дистрибутивность пересечения относительно объединения.

A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )

Необходимо убедиться, что множества, стоящие в левой и правой частях этого тождества, состоят из одних и тех же элементов. Сначала покажем, что множество левой части включается в множество правой части.

A ∩ ( B ∪ C ) ⊆ ( A ∩ B ) ∪ ( A ∩ C ).

Пусть x ∈ A ∩ ( B ∪ C ). Тогда по определению операции пересечения x ∈ A и x ∈ ( B ∪ C ). Если x ∈ B , то тогда x принадлежит и A и B и поэтому он принадлежит и их пересечению x ∈ ( A ∩ B ). Но поскольку x принадлежит объединению B и C , то он может принадлежать не только B , но и С и даже обеим этим множествам. Если x ∈ С , тогда он принадлежит и пересечению А и С , т. е. x ∈ ( A ∩ C ). Но отсюда можно видеть, что в любом из этих случаев x принадлежит к какому-то из множеств: либо ( A ∩ B ), либо (A ∩ C ), и тогда в соответствии с определением операции объединения x принадлежит и объединению этих множеств x ∈ ( A ∩ B ) ∪ ( A ∩ C ) и поэтому A ∩ ( B ∪ C ) ⊆ ( A ∩ B ) ∪ ( A ∩ C ).