Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

A с ={ x: x ∈ U, x ∉ A }.

В некоторых текстах дополнение A обозначается как A ’ или Ᾱ . На рис. 1.5(а) дополнение А с показано заштрихованной областью.

Операция разности множеств

Если подобным же образом рассматривать дополнение множества В до другого множества А , то можно получить операцию разности множеств А и В , обозначаемую как А\В , которая задает множество элементов, принадлежащих А , но не принадлежащих В , т. е.

А\В = { x: x ∈ A, x ∉ B }.

Иногда множество А \ В читается как « А минус В » и обозначается А – В . На рис. 1.5(b) разность А\В заштрихована.

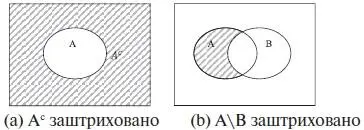
Рис. 1.5

Нетрудно заметить, что для любых двух множеств А и В выполняется тождество А\В = А ∩ В с.

Пример 1.5

Пусть универсальное множество U = N = {1, 2, 3, 4,…} является множеством натуральных чисел и пусть

А = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9},

и пусть D = {1, 3, 5, 7, 9,…}, множество нечетных чисел. Тогда дополнения

А с = {6, 7, 8, 9,…}, B c = {1, 2, 3, 9, 10, 11,…}, C c = {1, 2, 3, 4, 5, 6, 10, 11,…},

и разности множеств

А\В = {1, 2, 3}, А\C = {1, 2, 3, 4, 5}, B\C = {4, 5, 6}, C\B = {9},

B\A = {6, 7, 8}, A\D = {2, 4}, D c = {2, 4, 6, 8, 10,…}, множество четных чисел.

Симметрическая разность множеств

Симметрической разностью множеств А и В (обозначается A

B ) называется множество, которое состоит из элементов либо А , либо B , но не входящих в оба эти множества одновременно. Иначе говоря, это объединение этих множеств, из которого удалено их пересечение:

A

B = ( A ∪ B )\( A ∩ B ).

Можно также показать, что

A

B = ( А \ В ) ∪ ( В \ А ).

Например, пусть А = (1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8}. Тогда

А \ В = {1, 2, 3}, B \ A = {7, 8} и тогда A

B = {1, 2, 3, 7, 8}.

На рис. 1.6 на диаграмме Венна множество A

B заштриховано.

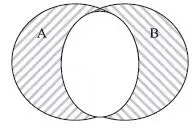
A

B заштриховано

Рис. 1.6

Операции над множествами позволяют образовывать из исходных множеств новые множества. При этом операция пересечения множеств применяется для различных практических задач, таких как классификация каких-либо объектов, анализ различного рода социологических опросов или исследований, анализ данных, из которых необходимо выбрать данные, характеризуемые заданными свойствами. Рассмотрим следующий пример. Пусть имеется список студентов группы, успешно решивших первую задачу контрольной работы (обозначим множество их фамилий как А ). Пусть также имеется список всех тех, кто успешно решил вторую задачу (множество В ), и всех тех, кто решил третью (множество С ). Если теперь потребуются сведения о тех, кто успешно решил и первую и вторую задачи одновременно, то необходимо будет выбрать тех, кто входит одновременно и в первый и во второй списки. Для этого надо найти новое множество, являющееся пересечением исходных множеств А и В , т. е. найти множество А ∩ B. Однако это множество не содержит информации о том, решили или нет данные студенты третью задачу. Ясно, что для этого потребуется найти еще одно множество, являющееся пересечением всех трех множеств, т. е. множество А ∩ В ∩ С .

Предположим теперь, что необходимо составить такой список, в котором присутствуют фамилии студентов, которые решили первую и вторую задачи, но не решили третьей. В этом случае надо найти множество А ∩ В ∩ С с.

Рассмотрение подобных случаев приводит к понятию фундаментального произведения множеств.

Пусть имеется n различных множеств А 1, А 2, А 3, …, А n. Фундаментальным произведением множествназывается множество вида