Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

Пример 1.2

(а) Рассмотрим множества:

Х = {1, 2, 3, 4, 7, 8}, Y = {2, 3, 8, 9}, Z = {2, 8}.

Здесь Z ⊆ X и Z ⊆ Y, но Y не является подмножеством Х, поскольку имеет элемент 9, которого нет в множестве Х . Кроме того, поскольку эти множества определяют одну и ту же задачу, то все они должны принадлежать к универсальному множеству U и это множество U должно содержать по крайней мере следующие элементы {1, 2, 3, 4, 7, 8, 9}.

(в) Пусть N, Z, Q, R – множества, о которых упоминалось выше. Тогда

N ⊆ Z ⊆ Q ⊆ R .

(с) Каждое множество Х является подмножеством универсального множества U , поэтому по определению все элементы Х принадлежат U . Пустое множество Ø также является подмножеством Х .

(d) Если каждый элемент А принадлежит множеству В , а каждый элемент В принадлежит множеству С , тогда каждый элемент А принадлежит С , т. е. если A ⊆ B и B ⊆ C , тогда A ⊆ C .

(e) Если A ⊆ B и B ⊆ A , тогда А и В имеют те же самые элементы и А = В . Обратно, если А = В , тогда A ⊆ B и B ⊆ A , так как каждое множество является подмножеством самого себя.

Формально последние три примера можно записать следующим образом:

1) для любого множества А всегда Ø ⊆ A ⊆ U ;

2) для любого множества А выполняется A ⊆ A ;

3) если A ⊆ B и B ⊆ C , тогда A ⊆ C ;

4) A = B, только если A ⊆ B и B ⊆ A .

Если A ⊆ B и A = B , то A называют несобственным подмножеством B . Когда A ⊆ B и A≠B , т. е. в B содержится по крайней мере один элемент, которого нет в A , то A называют собственным подмножеством B и пишут A ⊂ B . Пусть, например,

A ={1, 2}, B = {1, 2, 3, 4, 5}, C = {5, 4, 3, 2, 1}.

Здесь A и B являются подмножествами C , но A – собственное подмножество, а B – несобственное подмножество C .

Диаграмма Венна позволяет получить визуальное представление множеств в виде замкнутых областей на плоскости. Универсальное множество представляется внутренними точками прямоугольника, а другие множества представляются точками кругов (или каких-либо других областей, ограниченных замкнутыми кривыми), лежащих внутри этого прямоугольника. Фактически эти множества являются подмножествами универсального множества и поэтому между ними может существовать взаимосвязь в том смысле, что они имеют общие элементы. Например, для двух множеств A и B возможны три случая взаимосвязи по отношению включения. Если эти множества не имеют общих элементов, т. е. множества не пересекаются, тогда диск, представляющий A, будет отделен от диска, представляющего B, как на рис. 1.1(а). Если A ⊂ B, т. е. все элементы A являются также и элементами B , тогда диск, представляющий A, будет полностью лежать внутри диска для B, как на рис 1.1(b) (в случае, когда A ⊆ B и A = B , диск, представляющий A, будет совпадать с диском для B ).

Третий случай взаимосвязи множеств A и B показан на рис. 1.1(с), при этом:

– некоторые элементы имеются в A , но их нет в B ;

– есть элементы B , которых нет в А ;

– есть элементы, которые принадлежат и A и B одновременно;

– есть элементы, которых нет ни в A , ни в B .

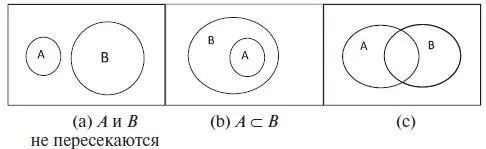
Рис. 1.1

Выводы диаграммы Венна

Аргументация в логике представляет собой полное или частичное обоснование какого-либо утверждения (заключения) с помощью других утверждений (посылок). Под выводомпонимается утверждение того, что заключение следует из посылок. Вывод называется правильнымтогда и только тогда, когда из конъюнкции посылок следует заключение, т. е. во всех случаях, когда посылки истинны, заключение тоже является истинным. Поскольку словесные утверждения по существу являются утверждениями о множествах, то поэтому их можно описывать диаграммами Венна.

Следовательно, диаграммы Венна можно использовать для проверки правильности выводов.

Пример 1.3

Показать, что следующий аргумент правильный:

A: Компьютеры, которые установлены на кафедре программирования, имеют LCD-дисплеи.