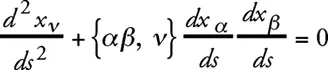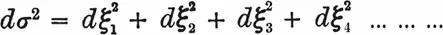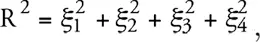Коллектив авторов - На плечах гигантов

Теория струн, разработанная по большей части уже после смерти Эйнштейна, породила новые модели зарождения Вселенной.

Из всего сказанного выше следует, что мне не удалось установить граничных условий для пространственной бесконечности. Тем не менее существует еще одна возможность, позволяющая обойтись без отказа, упомянутого в «б». Так, если бы можно было рассматривать мир в его пространственной протяженности как замкнутый континуум, то полностью отпала бы необходимость в подобного рода граничных условиях. Из дальнейшего будет видно, что и требование общего принципа относительности, и факт незначительности скоростей звезд совместимы с гипотезой пространственной замкнутости Вселенной. Однако для осуществления этого необходимо некоторое обобщение уравнений гравитационного поля.

Согласно общей теории относительности, метрический характер (кривизна) четырехмерного пространственно-временного континуума определяется в каждой точке находящейся в ней материей и состоянием последней. Из-за неравномерности распределения материи метрическая структура этого континуума должна быть крайне запутанной. Однако говоря о структуре пространства в целом, можно представить материю как бы равномерно распределенной по очень большой области пространства, так что ее плотность распределения становится чрезвычайно медленно меняющейся функцией. В данном случае мы поступаем так же, как геодезисты, которые крайне сложную в деталях поверхность Земли приближенно заменяют эллипсоидом.

Наиболее важное из того, что нам дает опыт о распределении материи, заключается в том, что относительные скорости звезд очень малы по сравнению со скоростью света. На этом основании я полагаю, что на начальном этапе в основу наших рассуждений можно положить приближенное допущение: пусть существует координатная система, относительно которой материю можно рассматривать находящейся в течение продолжительного времени в покое. По отношению к этой координатной системе контравариантный тензор материи T μν , в силу (5), имеет следующий простой вид:

(6)

Скаляр ρ (средней) плотности распределения изначально может быть зависимым от пространственных координат, но, предположив, что мир пространственно замкнут, мы можем сформулировать гипотезу о том, что ρ не зависит от места. Эту гипотезу мы положим в основу дальнейших рассуждений.

Что касается гравитационного поля, то из уравнения движения материальной точки

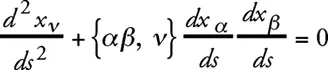
следует, что материальная точка в статическом гравитационном поле может находиться в покое только тогда, когда g 44не зависит от места. Так как, кроме того, мы для всех величин предполагаем независимость от временной координаты х 4, то для искомого решения можем потребовать, чтобы для всех x ν

Далее, как это обычно делается в статических задачах, примем, что

Остается определить те компоненты потенциала гравитационного поля, которые характеризуют чисто пространственно-геометрические свойства нашего континуума ( g 11, g 12, …, g 33). Из введенного допущения о равномерности распределения масс, создающих поле, следует, что и кривизна искомого метрического пространства должна быть постоянной. Таким образом, при заданном распределении масс искомый замкнутый континуум ( х 1, х 2, х 3при постоянном х 4) должен быть сферическим пространством.

Такое пространство можно получить, например, если исходить из евклидова пространства (ξ 1, ξ 2, ξ 3, ξ 4) четырех измерений с линейным элементом dσ . В этом случае

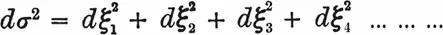
(9)

Рассмотрим в этом пространстве гиперповерхность

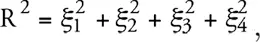
(10)

где R – постоянная. Точки этой гиперповерхности образуют трехмерный континуум – сферический объем с радиусом кривизны R .