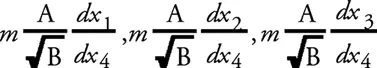
и для энергии (в случае покоя)
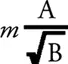
Из выражений для импульса следует, что играет роль инертной массы. Так как m – константа, связанная с точечной массой и независящая от положения этой массы, то при соблюдении условия, установленного для определителя, это выражение на пространственной бесконечности обращается в нуль только тогда, когда А стремится к нулю, а В стремится к бесконечности.
Рассмотренное поведение метрических коэффициентов g μν представляется нам как бы следствием относительности всякой инерции. Отсюда следует также и тот факт, что потенциальная энергия m√B точки на бесконечности становится бесконечно большой. Точечная масса никогда не может покинуть систему. Более детальное исследование показывает, что то же самое справедливо и для лучей света. Вселенная при таком поведении потенциала гравитационного поля на бесконечности не подвергалась бы опасности стать пустой, на что указывалось при обсуждении ньютоновской теории.
Упрощенные допущения о гравитационном потенциале, которые лежат в основе этих рассуждений, введены только для большей наглядности. Для описания поведения g μν на бесконечности можно найти общую формулировку, которая выразит суть без всяких ограничивающих допущений.
Пользуясь дружеской помощью математика Громмера, я исследовал центрально-симметричное статическое гравитационное поле, которое выражается на бесконечности указанным образом. Из заданного потенциала гравитационного поля g μν на основе уравнений гравитационного поля был вычислен тензор T μν энергии материи. Однако при этом оказалось, что для звездной системы подобного рода граничные условия никак не могут быть приняты. Недавно это вполне справедливо было отмечено также астрономом де Ситтером. Действительно, контравариантный тензор T μ энергии весомой материи имеет вид
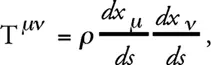
где ρ означает естественно измеренную плотность материи.
При надлежащем выборе координатной системы скорости звезд очень малы по сравнению со скоростью света. Поэтому ds можно заменить на 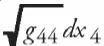 . Таким образом, все компоненты тензора T μν очень малы по сравнению с последней его компонентой, T 44 . Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √ В ) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для g μ ν в пространственной бесконечности не могут быть постулированы.
. Таким образом, все компоненты тензора T μν очень малы по сравнению с последней его компонентой, T 44 . Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √ В ) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для g μ ν в пространственной бесконечности не могут быть постулированы.
Неудача этой попытки указывает на две возможности: а) требовать, как в случае планетной проблемы, чтобы на пространственной бесконечности g μν при надлежащем выборе системы координат стремились к значениям

или б) не устанавливать для пространственной бесконечности никаких фиксированных граничных условий. В каждом отдельном случае следует особо задавать g μ ν на пространственной границе рассматриваемой области так же, как мы привыкли это делать до сих пор, задавая начальные условия.
Возможность «б» не соответствует какому-либо решению проблемы. Она означает отказ от ее решения. Правомерность такой точки зрения нельзя отрицать – в настоящее время ее придерживается де Ситтер [18]. Но я должен признаться, что мне трудно было бы пойти на столь большие уступки в этом принципиальном вопросе. С этим я соглашусь только в том случае, если все усилия найти удовлетворительные граничные условия окажутся тщетными.
Возможность «а» неудовлетворительна во многих отношениях. Во-первых, такие граничные условия предполагают определенный выбор системы отсчета, что несовместимо с духом принципа относительности. Во-вторых, эта возможность ведет к отказу от требования относительности инерции. Действительно, инерция материальной точки с естественно измеренной массой m зависит от g μ ν , но последние лишь очень мало отличаются от постулированных значений на пространственной бесконечности. Благодаря этому, несмотря на то что материя (находящаяся на конечном расстоянии) влияет на инерцию, но все-таки не обусловливает последнюю. Если бы существовала только одна материальная точка, то она, согласно этому представлению, обладала бы почти такой же инерцией, как и в том случае, когда она окружена всеми прочими массами нашего реального мира. Наконец, против этого представления нужно выдвинуть те же статистические возражения, которые выше были указаны для теории Ньютона.
Читать дальше

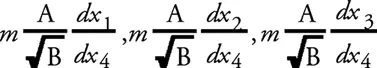
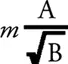
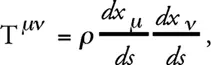
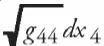 . Таким образом, все компоненты тензора T μν очень малы по сравнению с последней его компонентой, T 44 . Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √ В ) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для g μ ν в пространственной бесконечности не могут быть постулированы.
. Таким образом, все компоненты тензора T μν очень малы по сравнению с последней его компонентой, T 44 . Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √ В ) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для g μ ν в пространственной бесконечности не могут быть постулированы.











