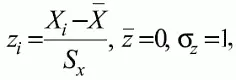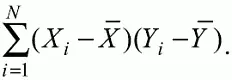Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

Вообще существует бесконечное множество нормальных кривых, отличающихся друг от друга значениями X̅ и S x , но все они объединяются общими свойствами, которые связаны с долями площади под кривой в пределах определенного числа отклонений. Из всех нормальных кривых наиболее удобна единичная, площадь под которой равна единице. Для нее среднее значение равно нулю, а стандартное отклонение единице.

Для преобразования любой нормальной кривой в единичную достаточно выполнить вычитание среднего значения X̅ из каждого индивидуального балла X i и разделить полученную разность на стандартное отклонение S x , т.е., применив формулу

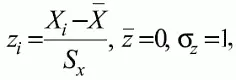
получим нормированное нормальное распределение со средним в нуле и единичным стандартным отклонением.

При разработке теста необходимо помнить о том, что кривая распределения индивидуальных баллов, получаемых на репрезентативной выборке, носит неслучайный характер. Она является следствием подбора трудности заданий теста. При смещении в сторону легких заданий большая часть студентов выполнит почти все задания теста и получит высокие индивидуальные баллы. При приоритетном подборе самых трудных заданий в распределении индивидуальных баллов получится всплеск вблизи начала горизонтальной оси. При оптимальной трудности теста, когда распределение оценок параметра трудности заданий имеет вид нормальной кривой, автоматически возникает нормальность распределения индивидуальных баллов репрезентативной выборки студентов, что в свою очередь позволяет считать полученное распределение устойчивым по отношению к генеральной совокупности и определить репрезентативные нормы выполнения теста.

Углубленный анализ качества теста, позволяющий сделать выводы о направлениях коррекции содержания отдельных заданий, связан с вычислением показателей связи между результатами испытуемых по отдельным заданиям теста. При оценке качества заданий важно понять, существует ли тенденция, когда одни и те же студенты добиваются успеха в какой-либо паре заданий теста либо состав учеников, добивающихся успеха, полностью меняется при переходе от одного задания теста к другому. Ответ на вопрос о существовании связи между двумя наборами данных получают с помощью корреляции.

Для выражения степени соответствия между наборами данных X и Y используется специальная мера, которая называется ковариацией. Смысл понятия «ковариация» удобно пояснить на примере результатов выполнения одной группой испытуемых двух тестов X и Y Пусть результаты по первому тесту X – это множество х i ( i = l, 2, …, Ν ) , а по второму тесту – Y i ( i = 1, 2, …, Ν ). Тогда для установления меры связи между результатами студентов по двум тестам необходимо сравнить положение каждого тестируемого по отношению к средним в распределении результатов по тесту X и по тесту Y. Степень соответствия результатов i -го испытуемого в первом ( X ) и во втором ( Y ) тестированиях будет проявляться в величине и знаке произведения отклонений ( X i – X̅ )( Y i – Y̅ ) , где X i , Y i – результаты i -го испытуемого в первом и во втором тестированиях соответственно ( i = 1, 2, … , N ); X̅, Y̅ — средние значения результатов по тестам X и Y, N — число студентов тестируемой группы.

Если результат i -го испытуемого намного выше или ниже среднего балла по обоим тестам, то произведение ( X i – X̅ )( Y i – Y̅ ) будет большим и положительным. Таким образом, при прямой связи значений X i и Y i ( i = 1, 2, …, N ) по тестам X и Y большой и положительной получится сумма всех произведений, т.е.

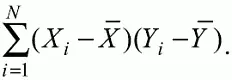
При обратной связи результатов тестирования, когда большинство значений X i выше (ниже) среднего X̅ по тесту X сменяются на значения Y i ниже (выше) среднего Y̅ по тесту Y, сумма

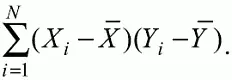
будет меньше нуля и велика по модулю в силу отрицательного знака всех или почти всех произведений ( X i – X̅ )( Y i – Y̅ ) . Наконец, если систематической связи между результатами студентов по тестам X и Y не наблюдается, знак произведения ( X i – X̅ )( Y i – Y̅ ) будет хаотически меняться. Вполне возможно, что для достаточно большой выборки испытуемых, положительные слагаемые будут уравновешиваться отрицательными и потому сумма произведений