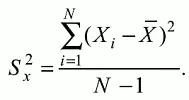Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

Подсчет дисперсии основан на вычислении отклонений X i – X̅ ( i = 1, 2, … , N ) каждого значения показателя от среднего арифметического в распределении. Для индивидуальных баллов значения отклонений несут информацию о вариации совокупности значений баллов N студентов, поскольку отражают меру неоднородности результатов по тесту. Совокупность с большей неоднородностью будет иметь большие по модулю отклонения, наоборот, для однородных распределений отклонения должны быть близки к нулю. Знак отклонения указывает место результата студента по отношению к среднему арифметическому по тесту. Для студента с индивидуальным баллом выше среднего значение разности X i – X̅ будет положительно, а для тех, у кого результат ниже X̅, отклонение X i – X̅ меньше нуля.

Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. В рассматриваемом примере матрицы сумма отклонений

Чтобы отрицательные и положительные слагаемые не уничтожали друг друга, каждое отклонение возводят в квадрат и находят сумму квадратов отклонений. Эта сумма будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой в случае близких результатов испытуемых по тесту.

Для рассматриваемого примера данных сумма квадратов отклонений

Величина суммы зависит также от размера выборки испытуемых, выполнявших тест, поэтому для сопоставимости мер изменчивости распределений, отличающихся по объему, каждую сумму делят на N – 1, где N – число студентов, выполнявших тест. Определяемая таким образом мера изменчивости называется исправленной дисперсией. Она обычно обозначается символом S x 2и вычисляется по формуле

(6.2)

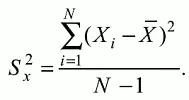
Кроме дисперсии, для характеристики меры изменчивости распределения удобно использовать еще один показатель вариации, который называется стандартным отклонением и вычисляется путем извлечения квадратного корня из дисперсии:

(6.3)

Для рассматриваемого примера данных тестирования

Свойства дисперсии и стандартного отклонения рассматриваются подробно в учебниках по статистике. Заинтересованному читателю можно порекомендовать, например, книгу Дж. Гласс, Дж. Стенли «Статистические методы в педагогике и психологии» [7].

Дисперсия играет важную роль в оценке качества тестов. Низкая дисперсия указывает на плохое качество нормативно-ориентированного теста, поскольку не обеспечивает высокий дифференцирующий эффект. Излишне высокая дисперсия, характерная для случая, когда все студенты отличаются по числу выполненных заданий, также требует переработки теста из-за существенного отличия вида распределения баллов от планируемой нормальной кривой. В процессе коррекции теста следует руководствоваться простым правилом: если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, а дисперсия растет, то это означает, что переработка приводит к повышению его качества.

Использование стандартного отклонения как меры вариации особенно эффективно для нормального распределения баллов испытуемых, поскольку в этом случае можно прогнозировать процент данных, лежащих внутри одного, двух и трех стандартных отклонений, откладываемых от центра распределения. В любом нормальном распределении приблизительно 68% площади под кривой лежит в пределах одного стандартного отклонения, откладываемого влево и вправо от среднего (т.е. X̅ ± 1 · S x ); 95% площади под кривой расположено в пределах двух S x откладываемых слева и справа от среднего ( X̅ ·± 2 · S ); 99,7% площади под кривой – в пределах трех S x по обе стороны от X̅ ( X̅ ± 2 · S x ) .