Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

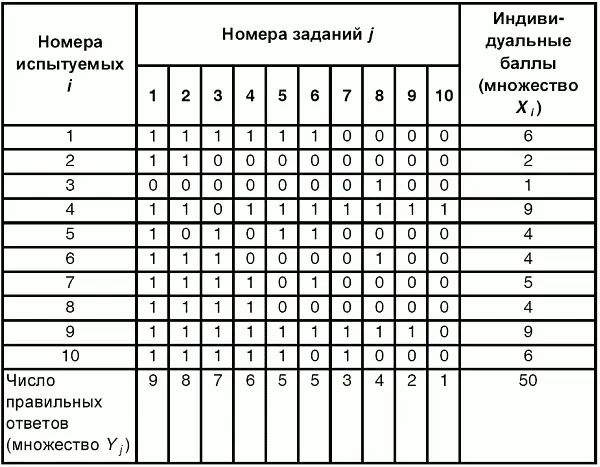
Пример матрицы наблюдаемых результатов, полученной при выполнения N ( N = 10) студентами n ( n = 10) заданий теста при дихотомических оценках (1 или 0) по заданиям приведен в табл. 6. 1.

Справа в вертикальном столбце содержатся индивидуальные баллы студентов Xi ( i = 1, 2, …, N ) , которые получаются суммированием единиц по горизонтали в каждом профиле ответов. Сложение единиц в столбцах по профилям ответов на n заданий теста позволяет получить числа Y j ( j = 1, 2, …, i ) , соответствующие количеству правильных ответов на каждое задание. С помощью матрицы можно выполнить ряд расчетов, интерпретация результатов которых позволяет сделать важные выводы относительно качества заданий теста и получить достаточно точные оценки параметра испытуемых в том случае, если тест соответствует определенным критериям качества.

Таблица 6.1Пример матрицы наблюдаемых результатов выполнения теста

Для анализа обычно используется упорядоченная матрица, в которой не только задания ранжированы по нарастанию трудности (см. табл. 6.1), но и баллы испытуемых расположены по убыванию или нарастанию сверху вниз (табл. 6.2).

По данным матрицы обычно проводят графическую интерпретацию распределений для трудности заданий и индивидуальных баллов испытуемых, которые представляют в виде полигона, гистограммы или сглаженной кривой (процентилей, огивы). Для больших выборок испытуемых (50 студентов и более) графическую интерпретацию предваряет формирование частотного распределения (табл. 6.3).

Таблица 6.2 Упорядоченная матрица данных тестирования

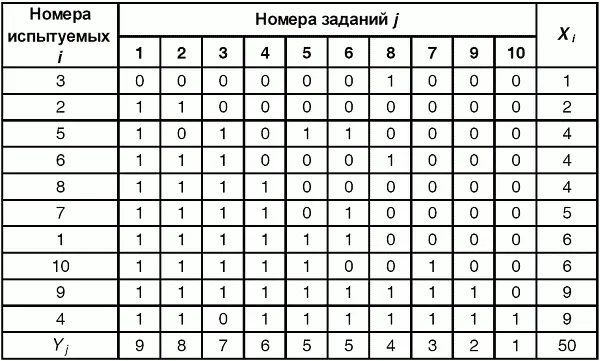
Таблица 6.3 Частотное распределение баллов

В табл. 6.3 содержатся только различные индивидуальные баллы испытуемых, взятые из последнего столбца матрицы эмпирических результатов выполнения теста и расположенные в порядке возрастания слева вместе с числом их повторений (f). Сумма всех частот для данного примера N = 1 + 1 + 3 + 1 + 2 + 2 =10, т.е. числу студентов в группе. Для очень большой группы в 100 или более студентов строят сгруппированное частотное распределение, в котором оценки объединяют в группы. Каждая группа называется разрядом оценок. В случае полного размещения оценок по разрядам говорят о распределении сгруппированных частот баллов студентов. Хотя четкого правила выбора количества разрядов нет, но обычно их число стараются варьировать в пределах от 12 до 15.

По ряду частотного распределения можно получить графическое представление результатов тестирования в виде гистограммы – последовательности столбцов, каждый из которых опирается на единичный (разрядный) интервал, а высота его пропорциональна частоте наблюдаемых баллов. Например, для рассматриваемого примера (см. табл. 6.3) гистограмма приведена на рис. 6.1. Середина столбца совмещается с серединой интервала разряда, который выбран длиной в 1 балл.

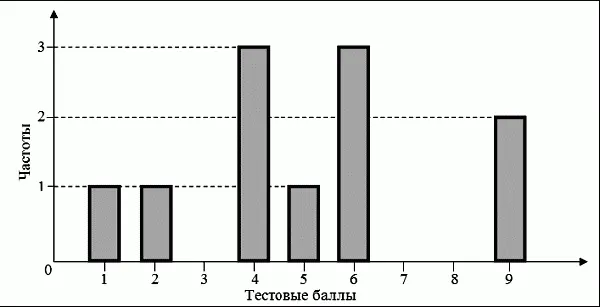
Рис. 6.1. Столбчатая гистограмма для распределения баллов в табл. 6.3

Для дальнейшего анализа данных оцениваются меры центральной тенденции в распределении результатов тестирования, которые предназначены для выявления той точки, вокруг которой в основном группируются все результаты выполнения теста. При анализе результатов тестирования можно использовать разные подходы к определению такой центральной точки. Наиболее простой способ основан на выявлении моды распределения и среднего арифметического баллов.

Мода – это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для данных табл. 6.3 модой является балл 4, потому что он встречается чаще (3 раза) любого другого балла. Конечно, не всякое распределение имеет единственную моду, их может быть две или больше. В случае существования двух мод распределение называется бимодальным. Если все значения баллов студентов встречаются одинаково часто, принято считать, что моды у распределения нет.

Среднее выборочное (среднее арифметическое) определяется суммированием всех значений совокупности и последующим делением на их число. Для индивидуальных баллов Χ 1 , Χ 2 , … , Х Nгруппы N испытуемых среднее значение X̅ будет: