РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
Здесь есть возможность читать онлайн «РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Год выпуска: 2007, ISBN: 2007, Издательство: Альпина Паблишер, Жанр: Прочая научная литература, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Издательство:Альпина Паблишер
- Жанр:
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг книги:4 / 5. Голосов: 2
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 80
- 1
- 2
- 3
- 4
- 5
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
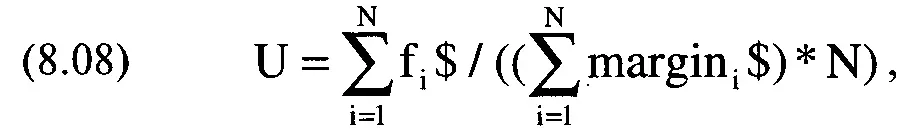
где U = верхняя граница дробного f, при которой можно торговать оптимальным портфелем без риска получения требования довнесения залога;
f$= оптимальное долларовое f для рыночной системы i;
margin $ = первоначальный залог для рыночной системы i;
N = общее число рыночных систем в портфеле.
Если U больше единицы, то приравняйте U к единице. Например, у нас есть портфель из трех рыночных систем со следующими оптимальными долларовыми f и первоначальными минимальными залоговыми требованиями (примечание: f$ являются оптимальными долларовыми f для каждой рыночной системы портфеля, они представляют собой оптимальные f рыночных систем, деленные на соответствующие веса в портфеле):
| Рыночная система | f$ | Первоначальный залог |
| А | $2500 | $2000 |
| В | $2000 | $2000 |
| С | $3000 | $2000 |
| Суммы | $7500 | $6000 |
В соответствии с уравнением (8.08) мы возьмем сумму всех f$ (7500 долларов) и разделим ее на сумму первоначальных залоговых требований (6000 долларов), умноженную на число рынков N:
U = $7500 / ($6000 * 3) =7500/18000 =0,4167
Таким образом, доля f не должна превышать 41,67% (если мы применяем стратегию динамического дробного f), т. е. следует производить переразмещение, когда отношение активного баланса к общему балансу больше или равно 0,4167.
Если вы все-таки применяете стратегию статического дробного f (несмотря на все ее недостатки), тогда максимальное значение используемой доли должно быть равно 0,4167. Такой подход сместит вас по геометрической эффективной границе портфелей с неограниченной суммой весов влево от оптимального портфеля, но вы будете настолько близко к нему, насколько только возможно, чтобы не столкнуться при этом с требованием довнесения залога. Для примера рассмотрим счет в 100 000 долларов. Если доля f равна 0,4167, то для каждой рыночной системы получим:
| Рыночная система | f$ | /0,4167= | Новое И |
| А | $2500 | $6000 | |
| В | $2000 | $4800 | |
| С | $3000 | $7200 | |
При счете в 100 000 долларов мы будем торговать 16 контрактами рыночной системы А (100 000/6000), 20 контрактами рыночной системы В (100 000/4800) и 13 контрактами рыночной системы С (100 000/7200). Итоговое требование к залогу для такого портфеля равно:
16 * $2000 = $32 000 20 * 2000 = 40 000 13 * 2000 = 26 000
Первоначальное требование залога $98 000
Отметьте, что с помощью формулы (8.08) вы получите максимально допустимую долю f (без риска сразу же столкнуться с требованием довнесения залога), при этом отношения рыночных систем друг к другу останутся без изменений. Следовательно, уравнение (8.08) задает разбавленный неограниченный оптимальный портфель, в котором отсутствует риск получения требования довнесения залога. Заметьте, если торговать на основе стратегии дробного f, значение, полученное из уравнения (8.08), является максимальной долей f, которую вы можете использовать (без риска сразу же столкнуться с требованием довнесения залога). Вернемся к нашему счету в 100 000 долларов. Предположим, когда вы открыли счет, на нем было 70 000 долларов. Далее, из этих первоначальных 70 000 долларов вы отвели 58 330 долларов под неактивный счет. Таким образом, вы начали торговлю с отношения между неактивным и активным балансом приблизительно 83 к 17 и далее торговали активной частью при полных значениях оптимального f. Теперь, когда счет равен 100 000 долларов, а неактивный баланс — 58 330 долларам, активный счет составляет 41 670 долларов, т.е. 0,4167 от общего баланса. Полученное значение задает максимальную долю, которую вы можете использовать (максимальное отношение активного баланса к общему балансу), без риска столкнуться с требованием довнесения залога. Вспомните, что вы торгуете полным f, т.е. 16 контрактами рыночной системы А (41 670/2500), 20 контрактами рыночной системы В (41 670/2000) и 13 контрактами рыночной системы С (41 670/3000). Итоговое требование залога для такого портфеля составляет:
16 * $2000 = $32 000 20 * 2000 = 40 000 13 * 2000 = 26000 Первоначальное требование залога $98 000
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема:
каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f$ = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ($5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом: разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения линейного программирования могут помочь агрессивному трейдеру. но решить такую матрицу будет достаточно сложно. Для заинтересованных читателей делаю ссылку на Чилдресса.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров»
Представляем Вашему вниманию похожие книги на «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.